글쓴이 : SOONDORI
이어가는 글. DIY보드 LPF 초입에서 보드 종단 RCA 단자까지를 관찰해 보았다. 각종 조정점은 건드린 게 없는 조건으로.
* 관련 글 : 튜너 동호인의 고수준 MPX 보드 (5), 제어 펄스에 대한 검토 #2
L+R과 L-R과 19Khz 등 모든 것을 커다란 냉면 그릇에 쏟아붓는 장면을 상상하면서…
더하기는 다 집어넣으면 되고, 빼기는 마이너스 부호가 있는 OP.AMP Inverting 핀으로 빼내면 된다. 나누기와 곱하기는… 그렇게 단순하게 처리되지 않음. 그래서 일단, 시뮬레이션 덧셈 회로만 구성하고 파형을 기록해 두면,
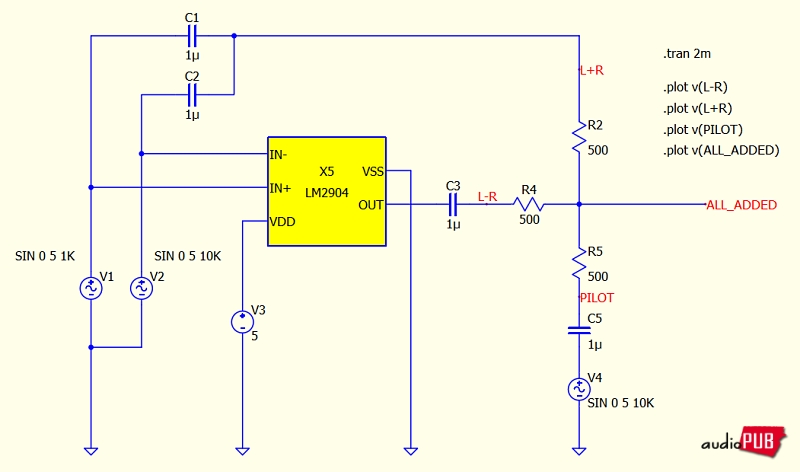
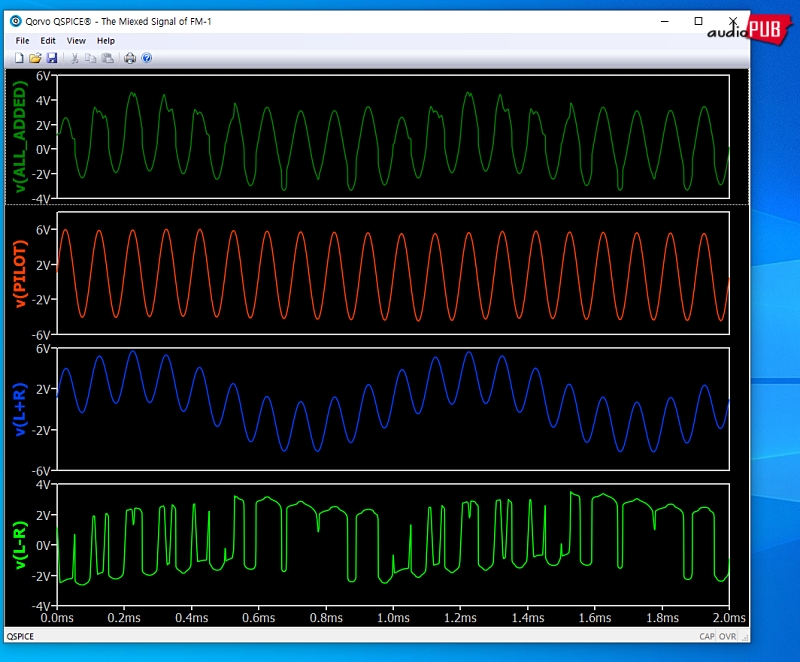
1) 느슨한 등락과 빠른 등락이 겹치는 L+R은 누구나 쉽게 이해할 수 있음.
2) 0.1초 이내 L-R의 가늠은, 인도 천재 소년만 할 수 있을 듯. 따져봐야 한다. 가장 높은 주파수 19Khz에 낮은 10Khz와 더 낮은 1Khz가 섞이면서 ALL_ADDED와 같은 파형이 나왔다. 여기서, 그것 기본 주기가 얼렁뚱땅 19Khz와 같다는 점에 유의.
(시간 흐른 후)
DIY 보드에 주입되는 신호는, a) 시간 축 우선으로 볼 때는 아주 작은 톱니가 보이는, 익숙한 그 싸인파이고, b) 주파수 축 우선인 FFT 모드로 보면, 당연히 1Khz와 19Khz 두 개뿐이다.
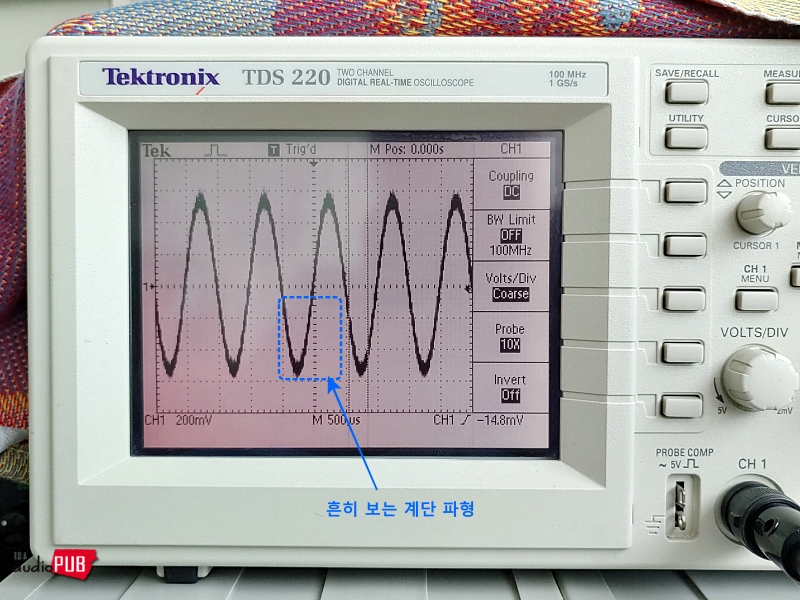
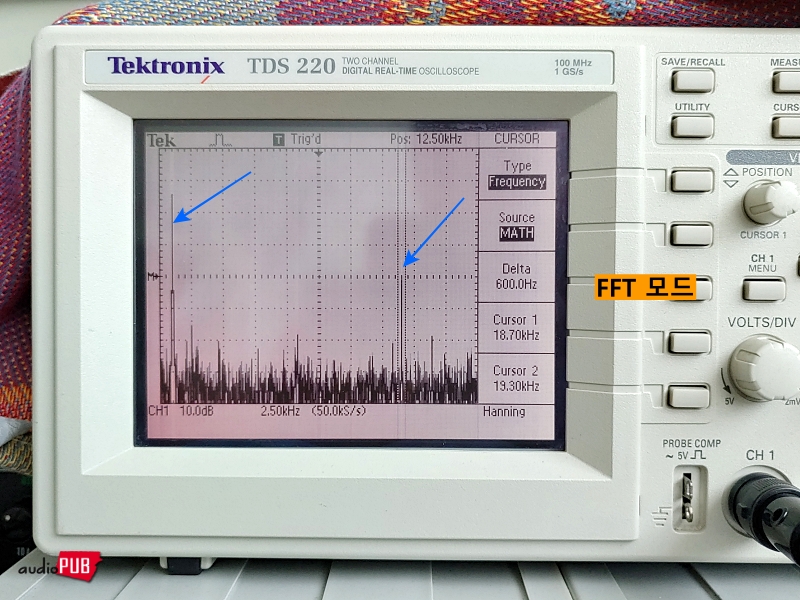
속내를 모르는 LPF는 일단 건너뛰고… 마지막 OP.AMP의 #2 (-) 입력 핀과 #1 출력 핀의 상태, RCA 출력 파형 등을 관찰해 보았다.
1) LPF 직후 = #2 입력핀 : 19Khz 파일럿톤이 깔끔하게 제거된 상태이다. NICE~!

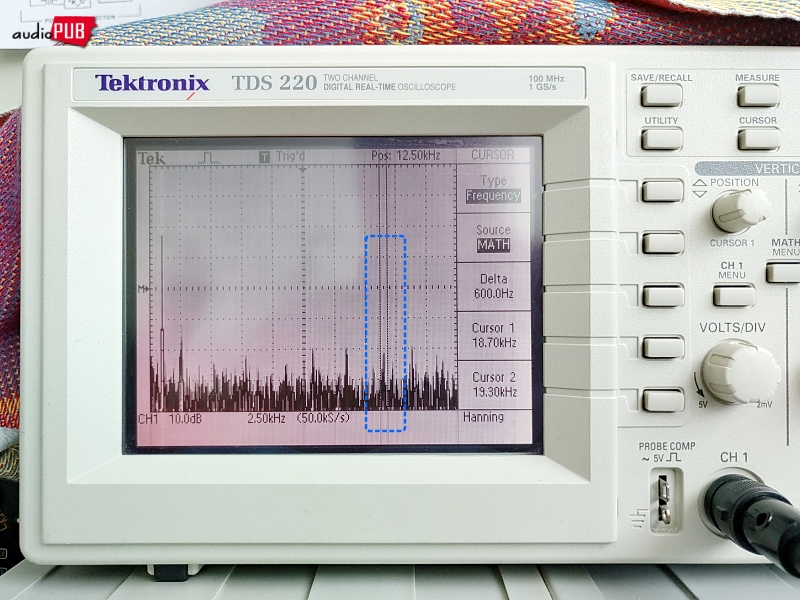
2) #7 출력 핀 : 응? 출력 핀에서 고조파 잡탕 잡음이 관찰되는 이유는… 디엠퍼시스 회로 C와 R의 작용 때문일 것으로 보고, 넘어감.

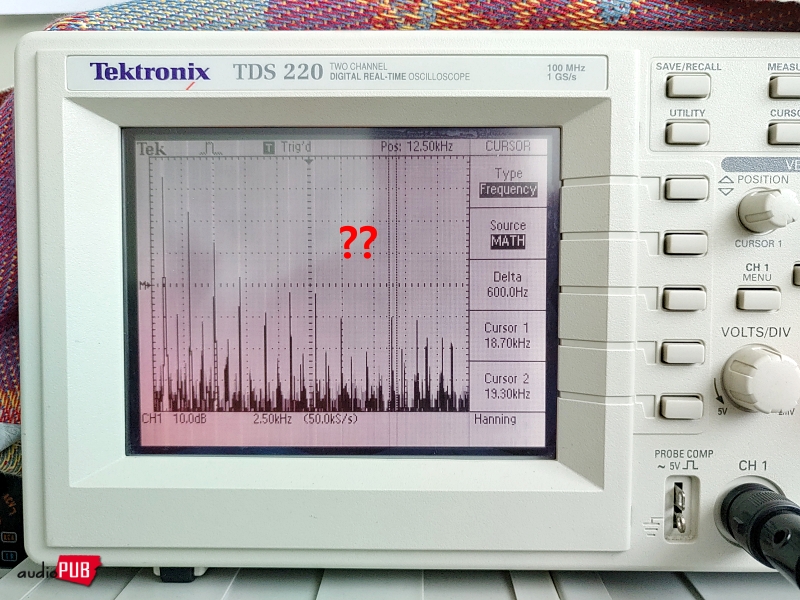
3) RCA 출력 단자 : 아주 깨끗한 1Khz 싸인파가 보인다. L+R ± (L-R) 처리에 있어서 (L-R) 전위가 제로이니까 즉, 신호가 존재하지 않으니까 L+R에 상당하는 1Khz만 보이는 것. 매우 당연한 일.
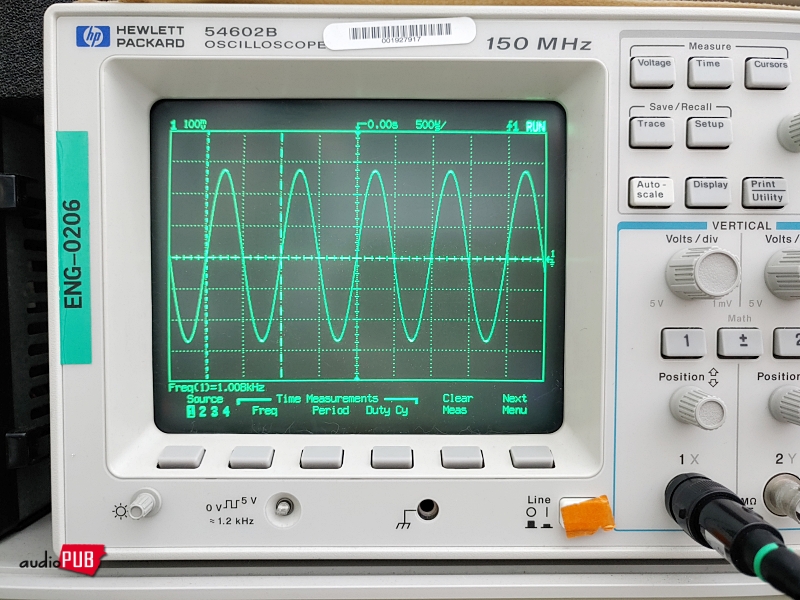
4) 그러고 나서, 조금 더 기능이 좋은 보조 펑션제너레이터를 가져다가 1Khz 출력을 1.6V(=+1.6V, -1.6V)로 맞추었을 때 그러니까 19Khz와 1Khz를 최대한 좋은 조건으로 주입했을 때의 THD는… 가볍게 0.1%.

참고로 캔우드 제시값은, 스테레오 모드 기준 Wide 0.08%@1Khz, Normal 0.2%, Narrow 0.4% → 강제 스테레오 분리 모드로 동작하고 있음에 점 유의. 그리고, 출력 전압을 최적화 시켰으므로… 역시, 유효 신호(~15Khz)와 파일럿톤과 38Khz 옆구리 신호의 강도 배분이 중요하다는 이야기가 된다.
그러니까 FM 스펙트럼 상 전위 배분율이 따로 정해져 있으니 그것을 잘 따라야… 단일 MPX IC의 경우는 스스로 알아서 처리하겠지만, 모든 게 눈에 보이는 디스크리트 방식 회로에서는 입력과 중간 조정점 등의 신호강도 배분이 중요한 검토점일 듯. 다음 작업에서는 뭘 잘 돌려야 하는데…
여기까지에서,
1) MPX 보드에 복합 신호를 주입하여, a) 스테레오 LED를 점등시키고, b) (L-R)이 없는 조건에서 RCA 단자까지 모든 것이 자연스럽게 처리됨을 확인하였다.
2) 이후 스펙트럼 배분을 최적화하고 JMPX 프로그램과 PC의 능력을 잘 조합하여… 거의 전문 계측기에 준하는 <PURE! 검파 후 신호>를 생성하고 주입한다면, 훨씬 더 좋은 수치가 나올 것이다.
3) 아무리 참조 회로가 있다고 해도, 이런 수준으로 구현하는 것은… DIY 세상에서는 정말 대단한 일이다.
다음 글에서 계속.
* 관련 글 : 튜너 동호인의 고수준 MPX 보드 (7), JMPX 프로그램과 스테레오 분리
○ 캔우드 문서 정보에서,
1) 65dBf라는 안테나 수신 전력 강도를 기준점으로 하고,
2) 안테나에서 RCA 단자까지의 모든 것을 종합 수치로 제시하고 있음에 유의해야 한다.
3) 뭐든 묶으면 수치가 나빠지니까… 부분품으로서의 MPX 성능 수치는 전체 수치보다 더 좋게 나올 수밖에 없음. 아주 아주 조금이라도 더.
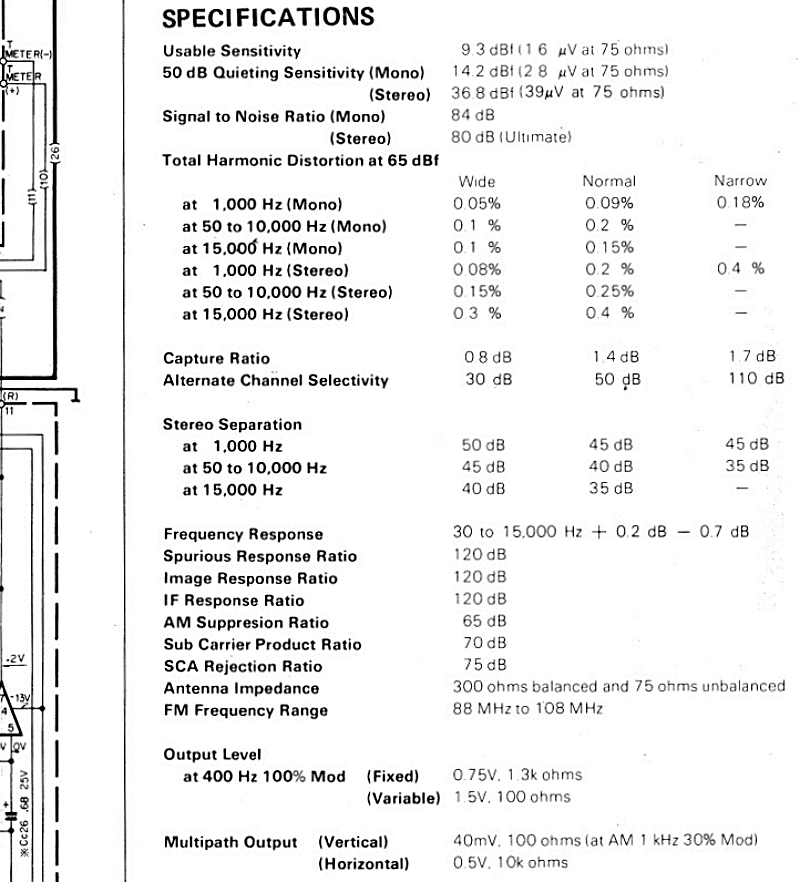
○ 기왕에 찍어 놓은 것이 아까워서 기록해 두기.
이러면 또, 글이 길어지는데…
적당히 양을 조절한 19Khz와 1Khz를 냉면 그릇에 넣고 비비면, 긴 주기의 1Khz에 조금 더 짧은 주기의 19Khz가 ‘묻어나는 현상’이 벌어진다. 그렇다고 하고… 그 냉면 그릇에 38Khz을 섞으면? 1Khz 주기에 19Khz 주기가 묻어난 것처럼 19Khz 주기 안에 38Khz 주기가 묻게 될 것.
그렇게 자꾸 뭘 더하면, 어떤 것의 안에 어떤 것이 들어가 있으면서… 마치 끝없이 세분화되는 프렉탈 파형처럼! (더하기, 곱셈, ADD이니까 그런 것)

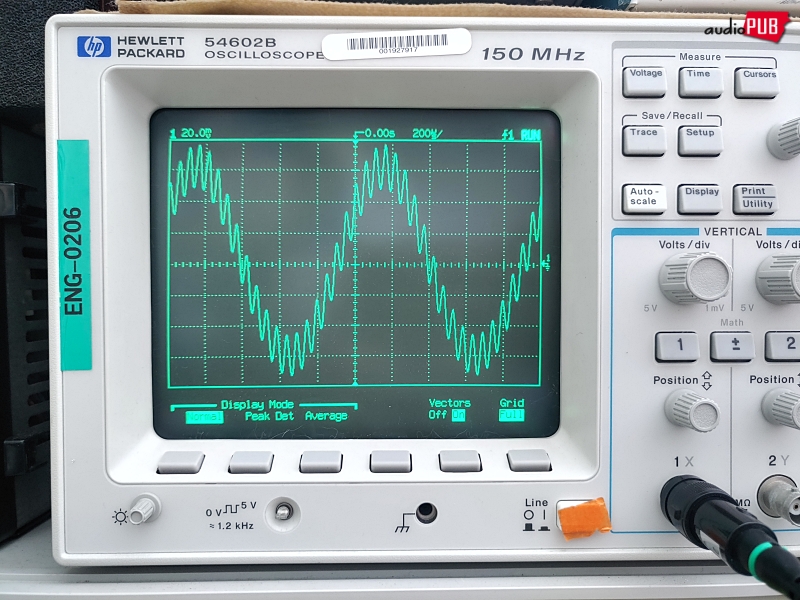
내친김에 위와 같은 1Khz+19Khz에 38Khz도 섞어보았다. 인도 천재 소년이 아니어도, 0.1초 만에 차이를 알 수 있음.
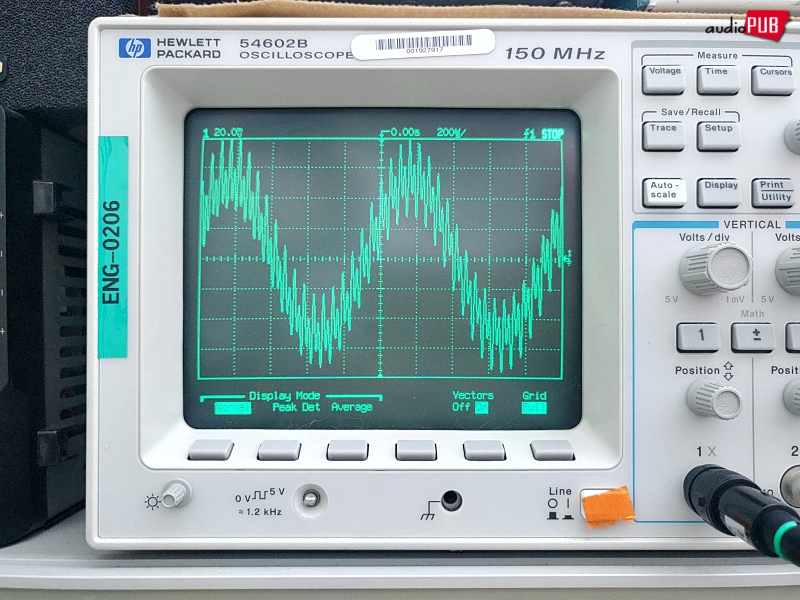

이렇게 뭘 자꾸 넣을 때, 기본파형 그러니까 주기가 가장 큰 것을 기준으로 점점 세밀해지는 현상을… “포락선(*)을 따라가며 주파수가 중첩된다”로 표현하면 될 것.
* 정말 그~지 같이 생뚱맞고 일제 냄새도 풀풀 나는듯한 ‘포락(包絡)’은, 영어 Envelope와 같은 말. 비유적 표햔으로 “신호가 담긴 봉투의 외곽선을 따라가면서”.




