글쓴이 : SOONDORI
모든 게 다 아날로그 디바이스社의 은밀한 PPL 광고 전술이다. 그러나 허구한 날 광고에 노출되며 살아가는 요즘에는, 이 정도는 약과이고 딴에는 매우 고마운 서비스. 아무튼, 그래서…
아래는 꽤 유용한 <BASIC 땡땡 문서> 중 일부.
* URL : https://www.analog.com/en/resources/technical-books/linear-circuit-design-handbook.html(Analog Devices Basic Linear Design 2편)
* 관련 글 : Analog Devices Basic Linear Design의 일부 (1), Mixers
섹션 2.11: 아날로그 곱셈기
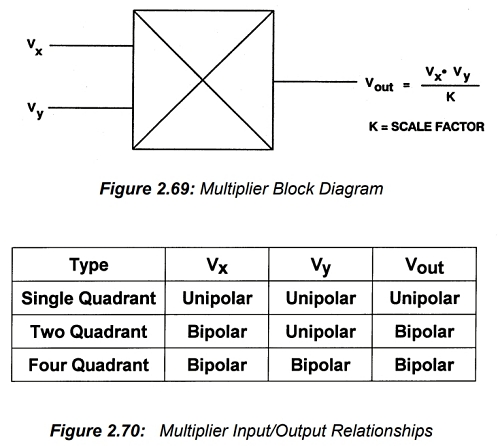
곱셈기는 두 개의 입력 포트와 하나의 출력 포트를 가진 장치입니다. 출력 신호는 두 입력 신호의 곱입니다. 입력 신호와 출력 신호가 모두 전압인 경우, 전달 특성은 두 전압의 곱을 전압 차원의 스케일링 계수 K로 나눈 값입니다(그림 2.69 참조).
수학적 관점에서 곱셈은 사분면 연산입니다. 즉, 두 입력 모두 양수 또는 음수일 수 있으며 출력도 양수 또는 음수일 수 있습니다. 그러나 전자 곱셈기를 생성하는 데 사용되는 일부 회로는 단극성 신호로 제한됩니다. 두 신호 모두 단극성이어야 하는 경우, 단일 사분면 곱셈기가 사용되며 출력 또한 단극성이 됩니다. 신호 중 하나는 단극성이지만 다른 하나는 어느 극성이든 가질 수 있는 경우, 곱셈기는 2사분면 곱셈기이며 출력은 어느 극성이든 가질 수 있으며(양극성입니다). 1사분면 및 2사분면 곱셈기를 생성하는 데 사용되는 회로는 4사분면 곱셈기에 필요한 회로보다 간단할 수 있으며, 4사분면 곱셈이 완전히 필요하지 않은 응용 분야가 많기 때문에 1사분면 또는 2사분면에서만 작동하는 정확한 장치를 찾는 것이 일반적입니다.
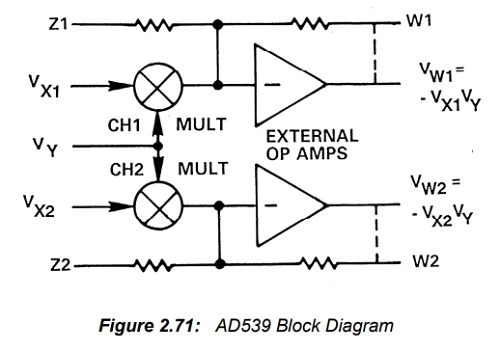
예를 들어 AD539는 광대역 듀얼 2사분면 곱셈기로, 5MHz의 비교적 제한된 대역폭을 가진 단일 단극성 Vy 입력과 곱셈기당 하나씩, 60MHz의 대역폭을 가진 두 개의 양극성 Vx 입력을 갖습니다. AD539의 블록 다이어그램은 그림 2.71에 나와 있습니다.
가장 간단한 전자 곱셈기는 로그 증폭기를 사용합니다. 이 계산은 두 수의 로그 합의 역로그가 두 수의 곱이라는 사실에 기반합니다. (그림 2.72 참조).
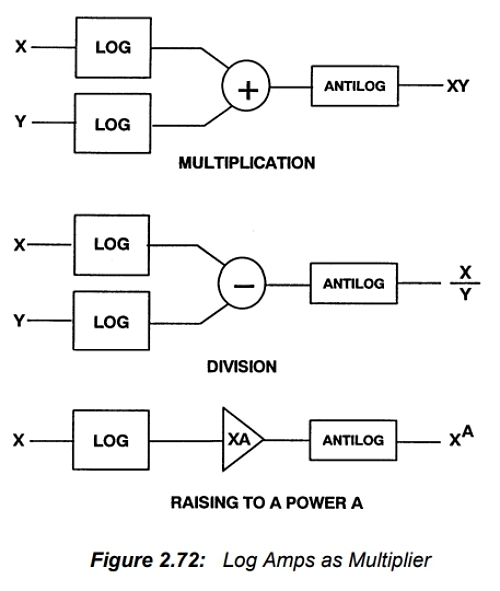
이러한 유형의 곱셈의 단점은 매우 제한된 대역폭과 단일 사분면 연산입니다. 훨씬 더 나은 유형의 곱셈기는 길버트 셀(Gilbert Cell)을 사용합니다. 이 구조는 1960년대 후반에 현재 아날로그 디바이스(Analog Devices)에 근무하는 배리 길버트(Barrie Gilbert)가 발명했습니다. 참고 문헌 1과 2를 참조하십시오. 실리콘 접합 트랜지스터의 컬렉터 전류와 트랜스컨덕턴스(이득) 사이에는 선형 관계가 있으며, 이는 다음과 같습니다.

이 관계는 그림 2.73과 같이 차동(롱테일) 실리콘 트랜지스터 쌍을 이용한 곱셈기를 구성하는 데 활용될 수 있습니다. 이 곱셈기는 (1) Y 입력이 Vbe에 의해 오프셋되고, Vbe는 Vy에 따라 비선형적으로 변하기 때문에 다소 성능이 좋지 않습니다. (2) X 입력은 Ic와 Vbe 사이의 지수 관계로 인해 비선형적입니다. (3) 스케일 인자는 온도에 따라 변합니다.
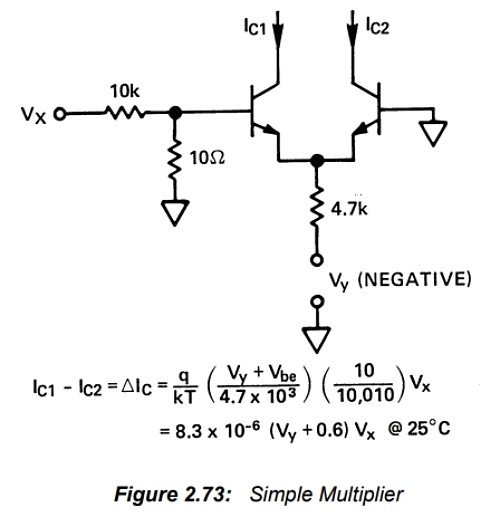
길버트는 전압이 아닌 전류를 사용하고 트랜지스터의 대수적 Ic/Vbe 특성을 활용함으로써 이 회로를 선형화하고 온도를 안정적으로 만들 수 있다는 것을 깨달았습니다(그림 2.74 참조).
길버트 셀의 X 입력은 차동 전류의 형태를 띠고 Y 입력은 단극성 전류입니다. 차동 X 전류는 다이오드로 연결된 두 트랜지스터에 흐르고, 대수적 전압은 지수적 Vbe/Ic 관계를 상쇄합니다. 또한, q/kT 스케일 인자는 상쇄됩니다. 이는 길버트 셀에 선형 전달 함수를 제공합니다.

현재 길버트 셀에는 세 가지 불편한 특징이 있습니다. (1) X 입력은 차동 전류입니다. (2) 출력은 차동 전류입니다. (3) Y 입력은 단극성 전류입니다. 따라서 셀은 2사분면 곱셈기에 불과합니다. 두 개의 셀을 교차 결합하고 두 개의 전압-전류 변환기를 사용하면(그림 2.75 참조) 기본 아키텍처를 AD534와 같은 전압 입력을 가진 4사분면 장치로 변환할 수 있습니다. 저주파 및 중주파에서는 감산기 증폭기를 사용하여 출력의 차동 전류를 전압으로 변환할 수 있습니다. AD534는 전압 출력 아키텍처이기 때문에 대역폭이 약 1MHz에 불과하지만, 이후 버전인 AD734는 10MHz의 대역폭을 제공합니다.
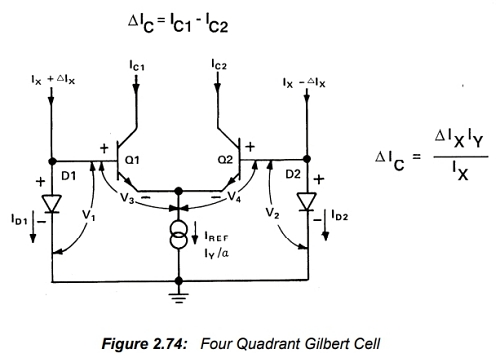
그림 2.75에서 Q1A와 Q1B, 그리고 Q2A와 Q2B는 두 개의 길버트 셀의 두 개의 코어 롱테일 쌍을 형성하고, Q3A와 Q3B는 두 셀 모두의 선형화 트랜지스터입니다.
그림 2.75에는 차동 전류-단일 종단 전압 변환기 역할을 하는 연산 증폭기가 있지만, 고속 애플리케이션의 경우 Q1과 Q2의 교차 결합 컬렉터가 차동 개방 컬렉터 전류 출력을 형성합니다(AD834 500MHz 곱셈기에서처럼). 초기형 곱셈기는 여러 트랜지스터와 전류의 정합에 의존합니다. 이는 모놀리식 칩에서 쉽게 구현할 수 있습니다. 하지만 최고의 IC 공정에서도 약간의 잔류 오차가 발생하며, 이러한 오차는 곱셈기에서 네 개의 DC 오차 항으로 나타납니다.
초기 길버트 셀 곱셈기에서는 이러한 오차를 칩 외부의 저항과 전위차계를 사용하여 조정해야 했는데, 이는 다소 불편했습니다. 칩 자체의 SiCr 박막 저항에 레이저 트리밍을 가능하게 하는 최신 아날로그 공정을 사용하면 제조 과정에서 이러한 오류를 트리밍하여 최종 소자의 정확도를 높일 수 있습니다. 내부 트리밍은 외부 트림팟의 경우처럼 고주파 성능을 저하시키지 않는다는 추가적인 이점이 있습니다.
트랜스리니어 곱셈기의 내부 구조는 필연적으로 차동 구조이므로 입력 또한 일반적으로 차동입니다(단일 종단 입력이 필요한 경우 입력 중 하나를 접지하는 것이 어렵지 않기 때문입니다). 이는 공통 모드 신호를 제거하는 데 편리할 뿐만 아니라 더 복잡한 계산도 수행할 수 있게 합니다. AD534(앞서 그림 2.71 참조)는 길버트 셀 기반 4사분면 곱셈기의 전형적인 예입니다. 곱셈기 모드에서 0.1%의 정확도, 완전 차동 입력 및 전압 출력을 제공합니다. 하지만 전압 출력 구조로 인해 대역폭은 약 1MHz에 불과합니다.
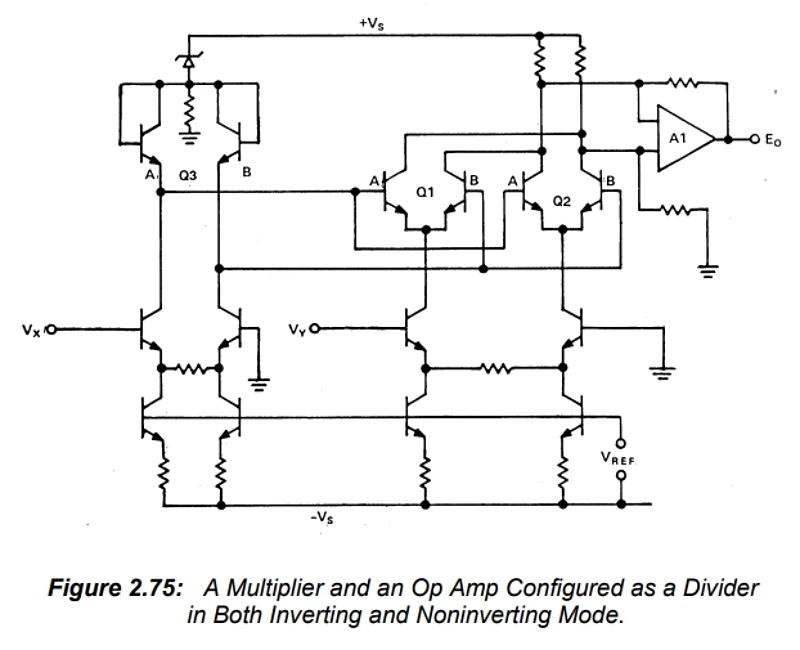
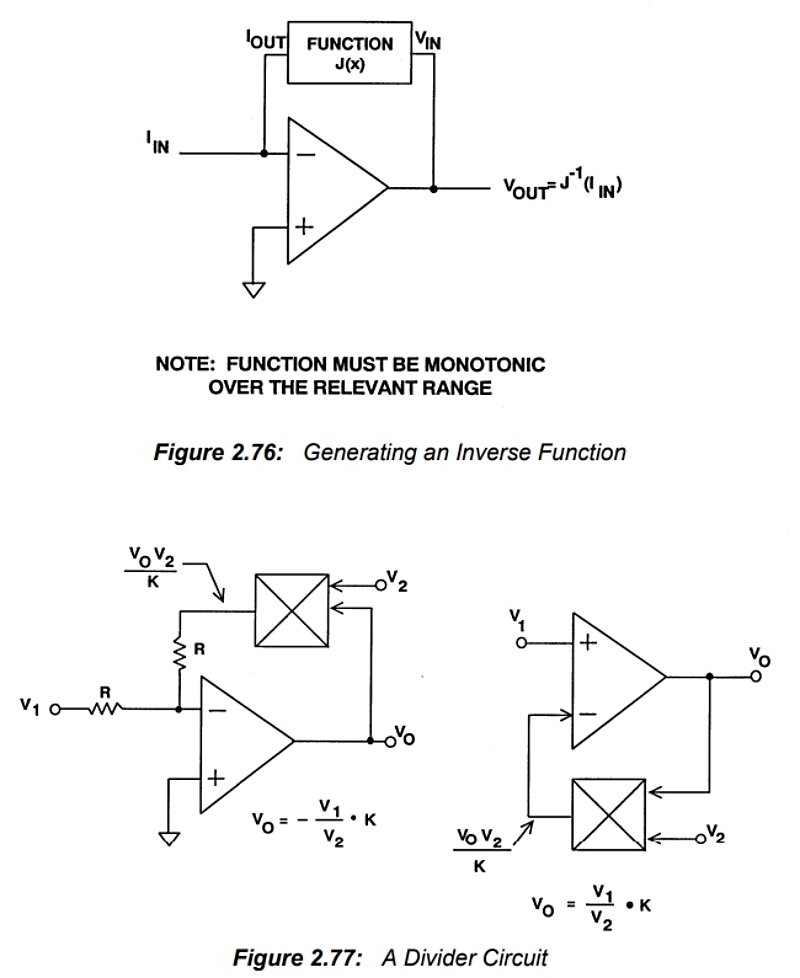
곱셈기는 연산 증폭기의 피드백 루프에 배치되어 여러 가지 유용한 함수를 형성할 수 있습니다. 그림 2.76은 음의 피드백 루프에 있는 함수 생성기가 역함수를 계산하는 아날로그 계산의 기본 원리를 보여줍니다(물론 해당 함수가 연산 범위에 걸쳐 단조적이어야 합니다).
고속 곱셈기는 RF/IF 섹션(섹션 4.3)에서도 논의됩니다.
* 관련 글 : Analog Devices Basic Linear Design의 일부 (3), Modulator




