글쓴이 : SOONDORI
자꾸 잔인한 ‘푸아그라’가 연상되는 푸리에 변환, 푸리에 급수… 뭐라고 하든, 그것은 모두 푸랑스 수학자 Jean-Baptiste Joseph Fourier(1768년~1830년)의 공식에 연결된다. 그가 이야기한 것의 핵심은,
1) 어떤 결과를 도출하는 함수가 있다고 하고,
2) 그 함수 값은 어떤 하위 싸이클(주기, Cycle) 성분으로 구성되며
3) 어떤 계산을 하면 그 함수에 담긴 싸이클 정보를 분리해낼 수 있고
4) 원한다면, 다시 그 함수의 결과값로 되돌릴 수도 있다
로 요약된다.
최초 아이디어는, 모든 수치를 다 검토하는 DFT(Discrete Fourier Transform). 그것이 음과 양 무한대를 다루어야 하니까, 버터플라이 형상으로 대표되는 모든 Tree를 다 탐색해야 하므로, 그리하여 연산 부담이 너무 극심하여, Log 장점을 취한 다음 공식 그리고 버터플라이 계산 맵의 절반만 취하기.
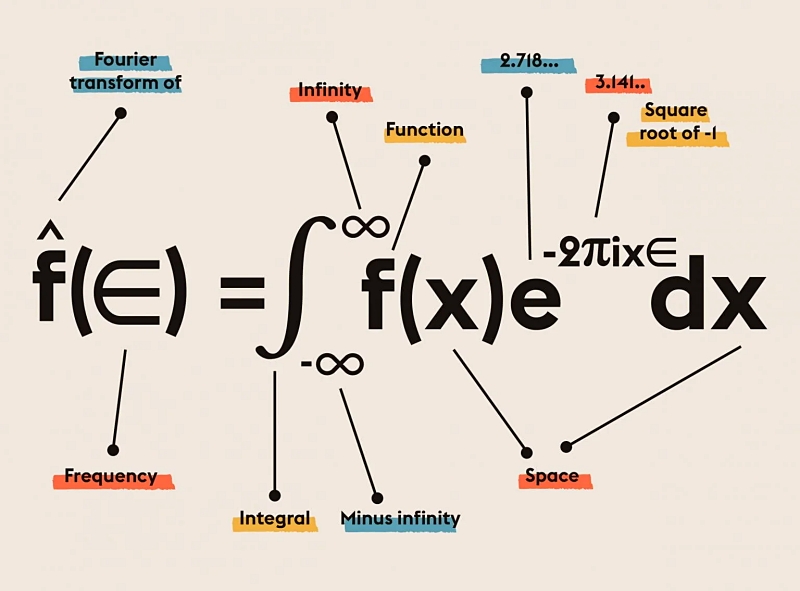
(▲ 이런 한 줄 수식을 적기 위해서, 그 앞쪽에서 별별 변환을 다 해야 한다. 수학 마인드가 있어야… SPACE가 언급된 것은, 푸리에가 시간 뿐만 아니라 공간의 개념을 적용하였기 때문에. 그래서, 임피던스 공식에 나오는 실수(Real Number)와 허수(Imaginary Number)의 복소수 개념이 등장하고…. 출처 및 추가 정보 열람 : https://abakcus.com/directory/fourier-transform/)
“절반떼기로 간단하게!”는 빠르다는 것이고 그래서 사람들은 ‘빠른 계산 푸리에 변환 기법’ 즉, FFT(Fast Frourier Transform)라고 이름을 붙였다. 그리하여 ‘주변에 보이는 모든 푸리에 장치’는 FFT를 쓴다.
<주변에 보이는 모든 푸리에 장치>의 대표 주자는 스펙트럼 애널라이저. 빠르다고 했지만, 그것은 상대적인 것이고… 연산용 RAM과 연산용 CPU와 빠른 클럭이 필요하니까 가격이 비쌀 수밖에 없음. (+어떤 연산 장치이든 부동소수점 연산이 가능해야 함. 정수 연산으로는 처리 불가. 부동소수점 연산 기능 내장 MCU는 정수연산 국한 MCU보다 비싸다) 물론, 요즘은 차고 넘치는 CPU 등 전산 자원이 있어서, 프로그램으로 FFT를 구현하고 즐기는 사람도 많다. 심지어 중국제 핸디 멀티미터에 FFT 기능이 들어가는 것이 그런 상황의 방증.

(▲ 프로그래밍 예시)
그렇게 신기한 푸리에 변환을 묘사적으로 표현하자면…
1) 라면 박스가 있다. 그 안에 삼양 라면과 스프가 100개 들어 있다.
2) 봉지를 뜯고 라면과 스프를 모두 꺼내서, 따로 마련한 아크릴 박스 안에 담는다. 아크릴 박스 왼쪽에는 라면만, 오른쪽에는 스프만.
3) 왼쪽 문으로 홍길동 씨가 들어와서 아크릴 박스 옆구리만 보면, “아? 스프만 잔뜩이네?” 또는 “아? 라면만 잔뜩이네?라고 할 것이다.
4) 아크릴 박스의 정면을 볼 수 있는 김삼숙 씨는, “아? 왼쪽에 라면이 있고 오른쪽에는 스프도 있네? 라고 할 것.

세상을 어떻게 바라보는가 즉, 보는 관점에 따라서 무엇이, 있거나 없다.
그 <바라보는 관점>을 도메인(Domain, 국면, 局面)이라고 한다. 아크릴 박스 앞쪽/뒤쪽/옆쪽이 도메인에 해당함. 종이 라면박스를 꺼내서 아크릴 박스 안에 넣은 것은 <어떤 변환> 행위이고, 아크릴 박스는 당연히 푸리에 변환기이며, 그리하여, “FFT는 시간 도메인을 주파수 도메인으로 바꾸는 것입니다”라고 말할 수 있고. 주파수 도메인의 관점은 김삼숙 씨의 시각과 같다. 종이 라면 박스는, 시간이 중요한 현실 세상.
비교 예시로서…사람이 생활하면서 사물을 접하는 방식이나 오실로스코프가 뭘 보여주는 방식은 Time Domain 기반이다. 즉, 시간이 흐르는 것에 종속되어 어떤 이벤트가 발생한다. 푸리에는 그것을, 주파수 축 기준으로 바뚜는, 참으로 혁신적인 아이디어를 소개했던 것.
말씀인 즉, 예전에 인간이 볼 수 없었던 삼라만상 관찰 방법 자체를 바꾼 것이다.
부처 님 마빡에 박혀있다는 제3의 눈을 통해서… 이제, 정경화 씨가 바이올린을 켜면 단음정 소리에 어떤 주파수가 담겨 있는지를 눈으로 볼 수 있다. 이제, NASA가 북한 땅을 찍으면 그 사진 안에 원폭 실험 X-선이 있는지 아닌지를 확인할 수 있다. 이제, 산업용 모터 소리를 녹음하고 FFT를 켜면, 메인 베어링에서 어떤 문제의 주파수가 생성되는지 여부를 확인할 수 있다.
빈티지 오디오 DIYer의 관점에서는 오로지… 어떤 장치의 FFT 버튼을 누르는 것으로 끝. 그러면 푸리에 변환기가 획득 신호를 조작하여… 라면 박스를 열고 신호를 분리해서 아크릴 박스에 넣어 준다. 사람이 볼 수 있는 곳으로 Domain을 달리하여 가져다주니까, 젓가락 들고 먹으면 됨.

* 관련 글 : LIG NEX1의 각종 스펙트럼 애널라이저, Made in Korea
그렇게 매우 강력하고 생각보다 매우 가까이 있는 FFT를 옆에 두고, 빈티지 오디오 세상에 시선을 돌리면…
1) FM 튜너
RF 수신 장치를 다루는 글에서 흔히 보게 되는 다음 그래프는, FFT로 작성된 것이다. 그림을 그리기 전에 누군가 어떤 장치로 관찰했다는 뜻.

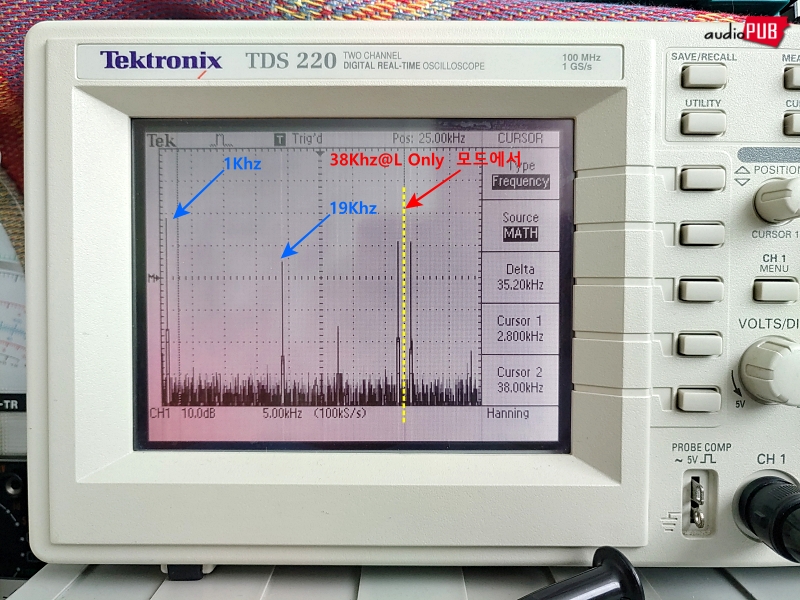
2) FFT와 버터플라이 맵, 두 벌 파형, SSB 아이디어
두 개 신호를 믹스하면 다음과 같이 두 개의 2차 파형이 생성된다. 이것이 Full Version이다. 중심축을 기준으로 왼쪽에도 파형이 있고 오른쪽에도 있고. 어떤 글, 어떤 문서에서도 그렇게 표현한다. 그것은 앞서 언급한, “푸리에변환이 버터플라이 트리-맵을 탐색한다”에 연결되어 있음. “잘만하면 나비 형상 아니어유?”
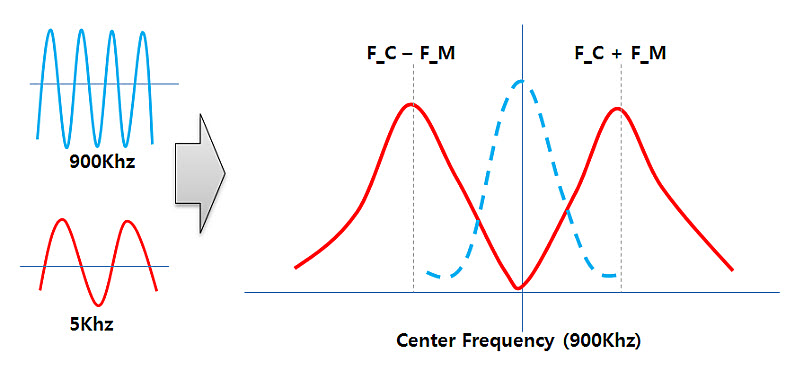
오른쪽 파형을 기준으로, 똑같은 모습의 왼쪽은 있으나마나, 쓸모 없는 것, 의미 없는 것. 그래서 영상 주파수 또는 Image Frequency라고 한다. 왼쪽을 기준으로 보면 오른쪽이 그런 것. 아무튼, 대칭이기 때문에 유효 정보가 두 벌 있는 셈이기에…
* 관련 글 : National R-1016 AM 포켓 라디오 (5), 발진회로와 IF
– HAM 세상에서는 SSB(Single Side Band) 개념을 적용하고 하나만 다룬다. 하나만 다루면, 1/2만큼 RF 방사 에너지를 줄일 수 있으니…무선 통신 여부에 삶과 죽음이 갈리는, 간당간당 배터리를 쓰는 군용 무전기에서는 매우 크리티컬한 주제.
– FFT 장치가 모든 것의 대칭 정보 중 1/2만 보여줘도 충분하다. 두 벌 다 보여주면 오히려 헷갈릴 것임.
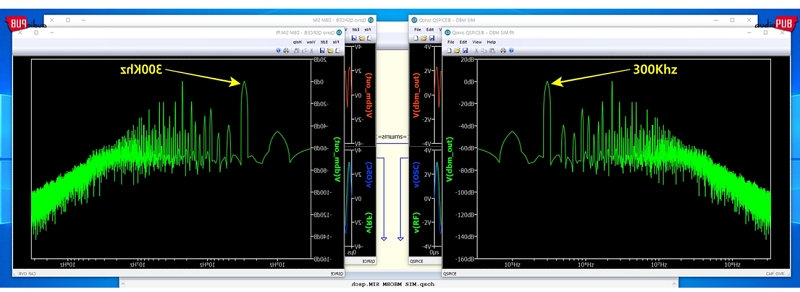
(▲ 두 개 신호를 MIX하는 경우. 그러면 F_center ±f_x 2종 주파수가 나온다. 누구도 모르는 왼쪽 세계에도 똑같은 형상이… 예시 시뮬레이션은 1/2만 보여주고 있었음.)
* 관련 글 : Double Balanced Mixer 동작 시뮬레이션
3) FFT와 보드선도
필터를 이야기할 때 반드시 등장하는 보드선도(Bode Plot) 역시 FFT가 개입된 것.
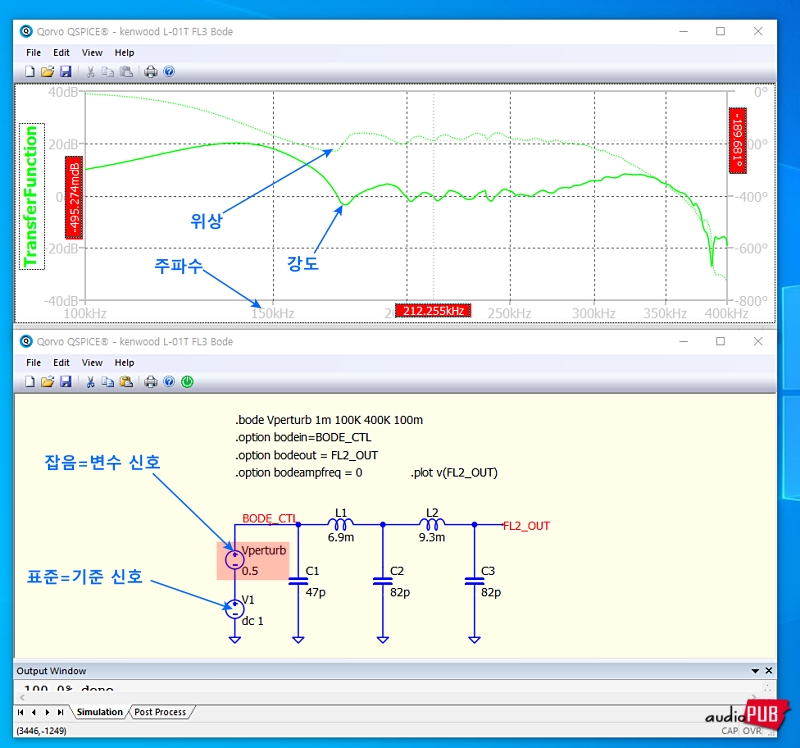
* 관련 글 : 오디오 시스템 평가의 기본 잣대, Bode Plot
참고로, PCD 검파회로 동작을 보여주는 다음 파형은, FFT 표현이 아니라 디지털 오실로스코프가 트리거점을 잘 잡아서 정지 상태로 고정한 것. 실제 신호는 시간축의 왼쪽에서 오른쪽으로 시간 경과에 의해 쭉~쭉~ 흐르고 있음이다. 착각 금물.
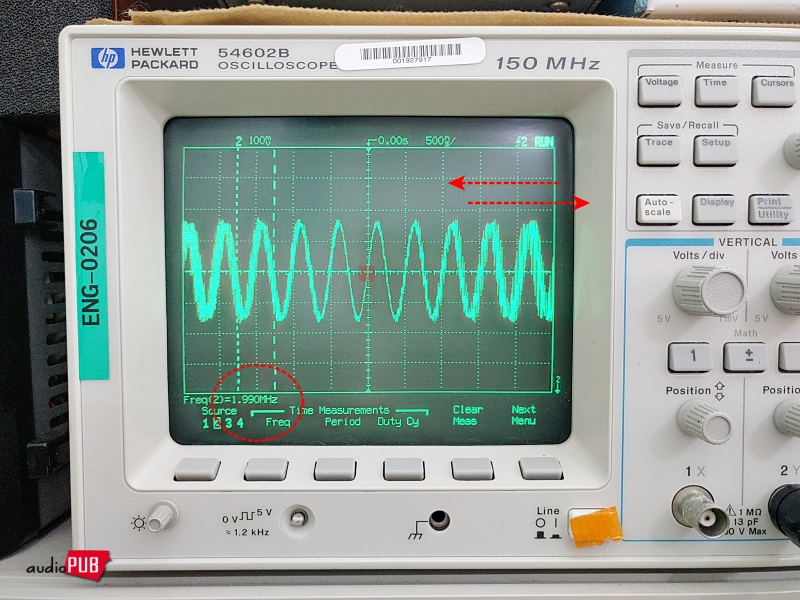
* 관련 글 : Kenwood L-01T FM 전용 아날로그 튜너 오버홀 (9), 펄스 카운터 검파 회로
4) 하드웨어적 구현
또 참고로… 위에 보이는 TEK 제품과 HP 제품 두 가지는, 모두 FFT 기능이 포함되어 있다. 아날로그 오실로스코프에는 당연히 없음. 다른 디지털 오실로스코프에는 있거나 없거나. 그리고… 옵션 수준에서 작동하기에 제대로 된 스펙트럼 애널라이저의 정보 제공 수준에 비할 게 아니다.

* 관련 글 : Tektronix TDS2MM, FFT 확장 모듈
“버튼만 누르면 됩니다!”, “푸리에 변환이 없었다면, 구글 유튜브와 스마트폰은 없다!”
푸리에 변환이 적용되는 사례 중심으로, 다음 글에서 계속. (표제부 사진 출처 : https://www.thinksrs.com/products/sr770.html, https://news.cnrs.fr/articles/joseph-fourier-is-still-transforming-science)
[ 관련 글 ]
빈티지 세상과 미래 세상을 움직이는 푸리에 변환 (2)
오디오의 주파수와 푸리에 변환 (1)
오디오의 주파수와 푸리에 변환 (2)
[ 첨언 ]
이 글은… 2025년 8월 14일자, JK LEE 님의 댓글 때문에 다시 정리하는 것.
“… 정말 쉽게 간단하게 sample 회로로 설명하는 글로도 쉽게 이해가 잘 안 갑니다. 주파수 대역별로 구분하지만 스코프로 시간대로 펼쳐지는 실제 신호는 합쳐진 신호라서 아무리 시각적으로 설명하는 글에서도 전공자가 아닌 이상 이해가 힘듭니다. 초심자가 도해식으로 쏙 이해할 수 있는 것 없을까요?…”
오실로스코프 화면(=종이 라면 박스)과 푸리에 변환기의 화면(=아크릴 박스)은 완전히 다른 것. RF를 다루는 글 대부분은, 단어 ‘Spectrum’을 중심으로 말을 풀어갈 수밖에 없기 때문에 푸리에 연산된 파형을 예시로 사용함.
칠판 그림이 예뻐서…