글쓴이 : SOONDORI
앞서 푸리에 변환기를 ‘라면과 스프를 담은 아크릴 박스’라고 했으니… 그 안에 무엇을 집어넣을 수 있는지가 곧 푸리에 변환이 얼마나, 어떻게 쓰이는지를 말해준다고 생각한다.
* 관련 글 : 빈티지 세상과 미래 세상을 움직이는 푸리에 변환 (1)
생각나는 대로, 애플리케이션 예시를 나열해 보면,
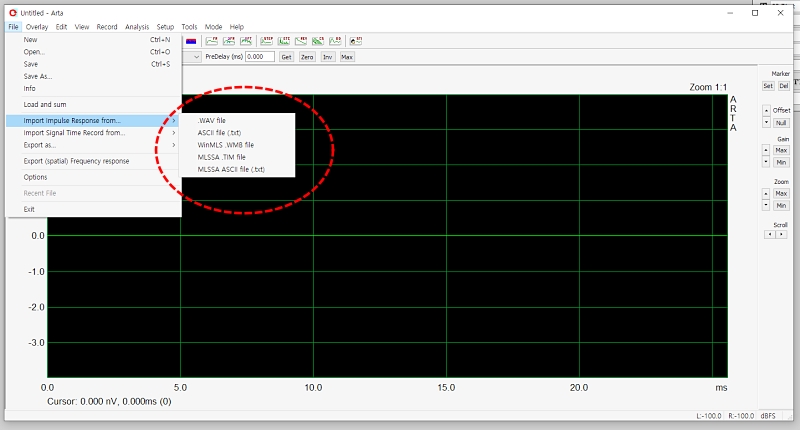
○ DIYer의 ARTA 프로그램 또는 웨이브스펙트라
ADC 디지털 데이터를 RAM에 집어넣고, 꺼내서 FFT 연산하는 것. 그러고는 적당한 그래프로 보여주기.

* 관련 글 : Technics SU-V6X 인티앰프 (6), 퍼포먼스 테스트 등
○ 스마트폰의 Spectrum 앱
MEMS 마이크로 집음 한 신호를 순수 프로그램만으로 처리.
○ RF 분야
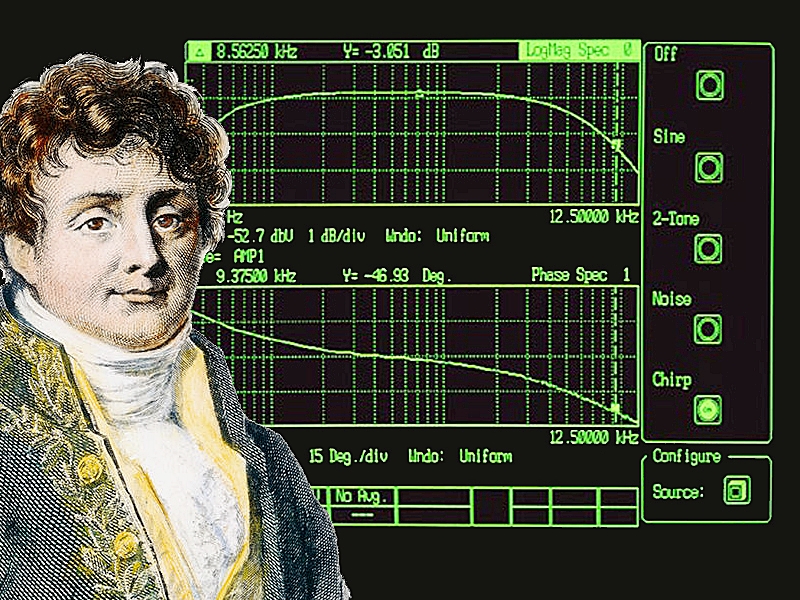
Spectrum이라는 단어를 쓰는 순간, 푸리에 변환이 개입된 것이다. X_Khz에서 Y_Mhz까지 범위를 정하고 FFT 처리하면, 그러니까 라면 박스를 먼저 정의하면, 아크릴 박스가 나오고, 사람이 무엇을 볼 수 있다. 더 간단하게는, X와 Y, 2 차원 그래프에서 아래쪽에 Hz 단위가 붙으면 무조건 FFT 연산형. 아래 고가의 Vector Network Analyer도 FFT 펑션을 포함한다. X축에 주파수가 표시되니까.

○ 우주탐사 분야
푸리에 변환을 가장 선호하는 조직이 NASA가 아닐까 싶음.
딥 스페이스 탐사에 있어서 다양한 분광 기술을 이용하고 그 분광 기술은 RF보다 진동수가 훨씬 높은 빛을, 스펙트럼으로 분해하는 것이다. 수집된 스펙트럼에 특정 Peak@주파수인 정보가 존재하면 그것이 곧 어떤 원자, 분자의 광 반응일 터. 그러면 수억 광년 떨어진 별의 조성이 무엇인지도 도출할 수 있음이니… 물론, 말만 그렇다. 온갖 우주 노이즈를 다 털어내고 순수 정보만 뽑아내는 기술이라는 것은, 그 수준을 상상을 할 수 없음.
아무튼 NASA 曰,
“… 고속 푸리에 변환 스펙트럼 분석 프로그램은 비행 후 우주선 원격 측정 궤적 데이터의 주파수 스펙트럼 분석에 사용됩니다. 디지털 알고리즘을 갖춘 이 컴퓨터 프로그램은 균일한 시간 간격에서 샘플링된 매개변수의 전력 스펙트럼, RMS 진폭 및 교차 스펙트럼을 계산할 수 있습니다…”
“… 정합 필터 검출 시스템의 유한 지속 시간 연속파(CW) 톤에 대한 감도를 윈도우형 이산 푸리에 변환(DFT) 시스템 및 이상적인 대역 통과 필터 뱅크 시스템의 감도와 비교합니다. 이러한 비교는 NASA의 외계 지능체 탐색(SETI) 마이크로파 관측 프로젝트(MOP) 하늘 조사의 맥락에서 이루어졌습니다. 다상 DFT 필터 뱅크 이론과 잘 알려진 윈도우형 DFT 프로세스와의 관계를 검토합니다. 다상 DFT 시스템은 다상 분기당 최소 8개의 필터 탭을 사용하여 이상적인 대역 통과 필터 뱅크에 근접합니다. 다상 DFT 방식을 사용하면 윈도우형 DFT 시스템보다 약 3dB의 감도 향상을 얻을 수 있습니다. 다상 DFT 시스템의 사이드로브 제거는 윈도우형 DFT 시스템보다 훨씬 뛰어나 무선 주파수 간섭(RFI)이 있는 경우 성능이 향상됩니다…”
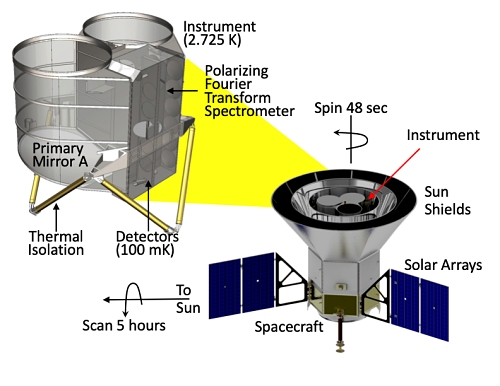
“… 원시 인플레이션 탐사선(PIXIE)은 우주 마이크로파 배경 복사(CMB)와 천체물리학적 전경의 스펙트럼 에너지 분포와 선형 편광을 측정하는 탐사선급 임무 개념입니다. 단일 극저온 푸리에 변환 분광기가 하늘을 외부 흑체 교정 대상과 비교하여, 28GHz에서 6THz까지 300개의 주파수 채널 각각에서 전체 하늘의 2.65도 직경 빔에서 스토크스 I, Q, U 매개변수를 약 200 Jy/sr 수준으로 측정합니다.
PIXIE 장비(그림 1)는 두 개의 입력 포트와 두 개의 출력 포트를 갖춘 편광 푸리에 변환 분광기(FTS)입니다. 입력 포트는 우주선의 회전축을 따라 동일한 방향으로 향하는 두 개의 빔을 생성하는 두 개의 비축 망원경에서 공급됩니다. PIXIE는 완전 개구 흑체 교정기를 탑재하여 100% 미만의 정확도로 절대 기준 광원을 제공합니다. 교정기는 두 빔 모두를 완전히 덮도록 배치하거나, 두 빔 모두 하늘을 볼 수 있도록 수납할 수 있습니다. 두 빔 모두 하늘을 볼 때, 장비는 비편광 방출을 무효화하여 프린지 패턴이 편광 방출의 주파수 스펙트럼만 인코딩합니다. 교정기가 두 빔 중 하나를 덮을 때, 프린지 패턴은 편광 및 하늘 방출의 절대 강도에 대한 정보를 모두 인코딩합니다…”
○ 연구용/스펙트로스코피
돈만 많으면, 다이아몬드 렌즈에, 티타늄 지그에, 강력한 X선에, 강력한 레이저에, 초고가 편광 렌즈에… 그런 식. 고수준 ADC 장비를 쓰고, 그리고 저~어기 방구석에 있는 고가의 PC 프로그램이 푸리에 변환 결과를 그래프나 점으로 보여주기.

(출처 : https://hal.science/hal-01520692/file/jeq-2017-01-0023_SI.pdf)
○ 산업용/진동분석
처음 접한 것이 20여 년 전. 그러니까, 이제는 특별할 것도 없음. 진동은 곧 오디오 신호와 같은 복합 주파수. 베어링 마모 등 기계적 이상이 발생하면, 진동 주파수가 달라지니까 그것의 세부 성분을 모니터링하고 또 그것을 참조 테이블에 비교하면, 정확하게 무엇이 문제인지를 파악할 수 있다. 이쪽 솔루션의 핵심은, 참조테이블의 정밀성. 이제는 코드 몇 줄로 구현할 수 있는 FFT가 아니고.
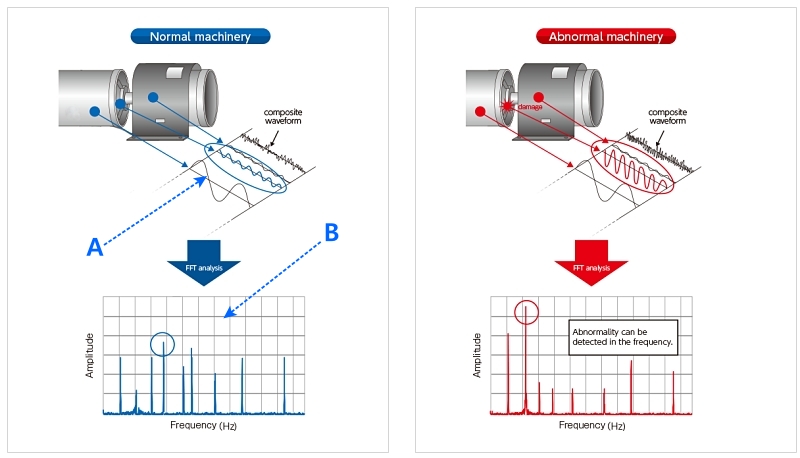
(▲ 이해의 방법은 매우 간단하다. A 파형은 오실로스코프 또는 고속 디지털 미터로 확인한 것으로 치부하여 넘기고, 푸리에 변환된 B 파형만 보면 됨. 푸리에 파형을 보기 위해서는, 버튼 하나만 누르면 됨. 출처 : https://we-are-imv.com/zh/support/library/vibration-measuring/vibration-measuring-04/)
○ 산업용/가짜 휘발유 판별
분광 기술을 뜻하는 Spectroscopy 활용 아이디어 중 하나. 대상 유류에 특정 광을 조사하고, 반사광 스펙트럼을 분석한다. 지표 인자는 톨루엔의 Peak. 톨루션 Peak 정보가 참조 테이블의 것과 부합하지 않으면 가짜. 부합하면 진짜.
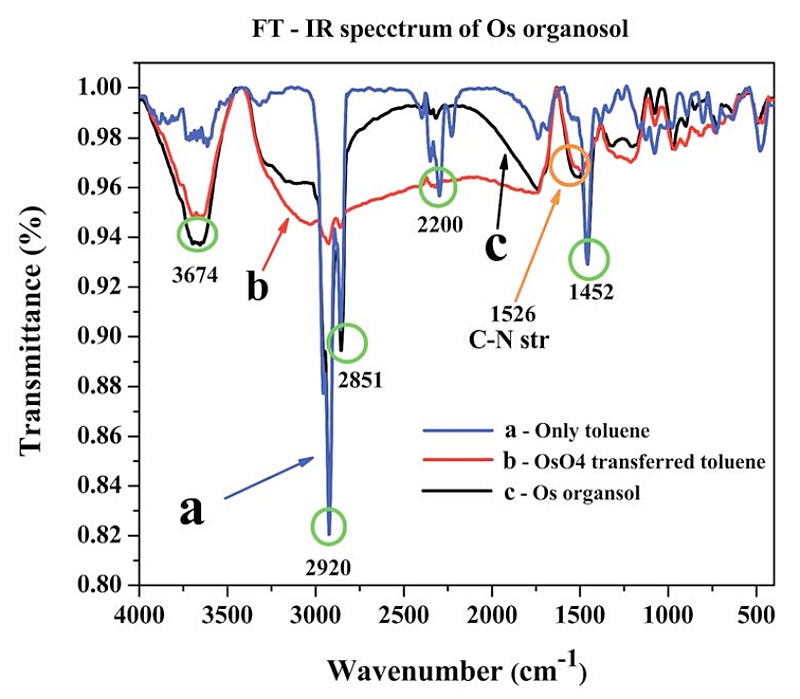
(출처 : https://www.researchgate.net/figure/The-Fourier-transform-infrared-FT-IR-spectrum-of-toluene-OsO-4-transferred-toluene-and_fig5_270817312)
○ 영상처리
이미지의 수직을 푸리에 변환 & 이미지의 수평을 푸리에 변환한 예.

(출처 및 추가 정보 열람 : https://medium.com/ntust-aivc/opencv-fourier-transform-d9811aaac2d5)
(▲ 영상 후반부, 마릴린 먼로와 아인쉬타인 얼굴의 합성 이미지가 나오고, Low Frequency와 High Frequency가 언급된다. 두 이미지의 Low와 High를 구분하고 양자를 적절히 혼합을 하려면, 역시 세부 스펙트럼을 분리해야 하고 그러려면 푸리에 변환이 필요함)
○ 엔지니어링과 관련 없는 세상의 패턴 분석
다음은 어떤 연구 논문의 이야기.
“… 금융 데이터에 대한 푸리에 변환의 적용 및 공분산 추정 검토” 논문에서 저자는 두 가지 모델, 즉 전통적인 자기회귀 모델과 푸리에 변환을 통해 수정된 모델을 통해 계산된 추정값을 비교하는 실험을 수행했습니다…” (출처 : https://www.deanfrancispress.com/index.php/fe/article/download/270/FE000492.pdf/1207)
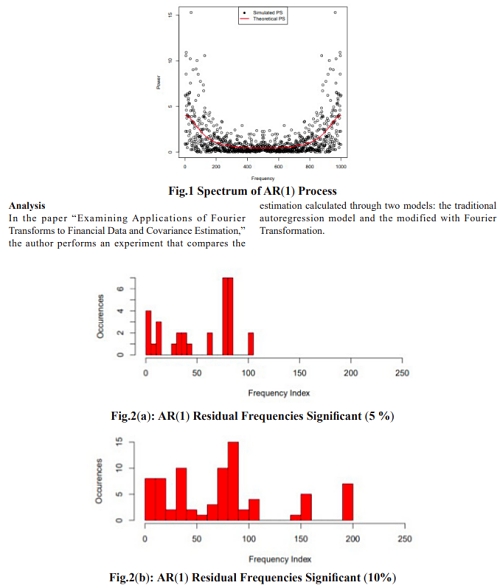
또다른 언급.
“… 1976년이었던가? 본저자는 당시 인기가 있던 IBM주식의 주가를 피어리오드그램(periodogram)을 사용해서 분석한 적이 있었다. 그로부터 43년이 지난 2019년 서울대학교 수학과에서 포스트닥터를 하던 김박사가 찾아와서 주가데이터에서 주기를 찾아내는 문제에 관해서 질문을 했다. 간단히 피어리오드그램(periodogram)을 설명해주고, 좀 더 자세한 것을 공부하고 싶으면 M.B. Priestley교수가 1982년에 쓴 Spectral Analysis and Time Series를 읽으라고 권유하였다. ‘퀀티터티브트레이딩을 하려면 Fourier해석과 FFT를 알아야 한다’는 말과 함께 … (출처 : 금융공학 IX – Fourier Analysis
for Financial Engineering, 최병선, https://s-space.snu.ac.kr…Financial…Engineering.pdf)
예를 들어 특정 지역 주민의 소비 패턴을 분석할 수도 있다. 고속도로 자동차 통행 패턴을 분석할 수도 있다. 즉, 빅 데이터에서 무엇을 뽑아내기 위해서, 빅 데이터 내 유형을 추출할 때도 푸리에 변환이 유용하다는 이야기.
뭐가 더 있을 것 같은데… 이쯤에서 정리하기를,
1) 철학으로 통하는 수학은, 모든 것을 떠받치는 학문이다. 수학 세상에 속한 푸리에 변환은 그렇게 모든 것 아니, 이 세상을 떠받치고 있다.
2) 음성신호나 93.1Mhz RF 주파수나 블루투스 2.4Ghz나 빛이나 뭐나… 또는 여러 사람의 움직임이나 Cash Flow로 정의되는 돈이나 함수 관계가 복잡한 정치나 어떤 사회나, 그런 모두는 ‘맥동’이고 맥동은 곧 주파수. 그렇게 주파수만 정의되면, 무조건 푸리에 변환을 할 수 있다.
한마디로 푸리에 변환은, 마른 북어와 같은 빈티지 오디오의 하위 범주에 불과한 FM 튜너에 국한될 수 없는, 어디에든 쓸 수 있는 명가의 보검이자 큰 사상이다.
그렇고…
다음 글에서, ARTA 프로그램으로 푸리에 변환하는 예시 사례를 정리. (사실은, ARTA가 웨이브스펙트라보다 더 좋다. 일단, 매뉴얼이 있고 무엇도 있고… )
* 관련 글 : 빈티지 세상과 미래 세상을 움직이는 푸리에 변환 (3)