글쓴이 : SOONDORI
호주의 오디오 전문 매거진, 일렉트로닉스 오스트레일리아 1990년 1월호에서.
* URL : https://archive.org/details/EA1990/EA%201990-01%20January/page/n155/mode/2up?view=theater
FM Bandwidth and Frequency Response
주파수 변조(FM)는 AM보다 더 넓은 대역폭을 필요로 하므로 더 높은 주파수 채널이 사용됩니다. 다양한 변조 조건에서 반송파와 측파대의 패턴을 조사하고 일반적인 FM 방송국의 특성을 살펴봅니다.
저희 FM(주파수 변조) 방송국이 모두 100MHz 정도의 VHF 대역에서 방송되는 이유가 궁금하신 적이 있으신가요? 특정 지역에서 특정 FM 방송국을 수신할 수 없는 경우가 있어 답답하셨을지도 모릅니다.
VHF 전송은 송신기와 수신기 사이에 가시선 경로를 선호하기 때문에 언덕이나 고층 건물이 있으면 음악 수신이 완전히 차단될 수 있습니다. 안타까운 점은 언덕과 건물이 있어도 HF 대역의 AM 방송 수신은 도시와 교외 어디에서나 쉽게 가능하다는 것입니다! 왜 FM 방송국은 HF 주파수에서 방송할 수 없는 걸까요? 사실 HF 대역은 이미 AM 방송국으로 가득 차 있어서 여유 공간이 없습니다. 하지만 이것이 정답은 아닙니다.
FM 방송국이 상당히 높은 반송 주파수에서 작동해야 하는 데에는 타당한 기술적 이유가 있습니다. 바로 전송 대역폭의 문제입니다! FM 방송국을 수용하려면 얼마나 넓은 RF 채널이 필요할까요? 좋은 질문입니다! 하지만 계속 읽어보세요…
FM 용어
이전 장에서 몇 가지 용어의 정의를 살펴보았습니다. 반송파 중심 주파수를 나타내는 데 fc를 사용합니다. 변조가 없다면 방송국은 단순히 주파수 fc의 사인파 신호를 전송합니다. 하지만 오디오 신호에 의해 주파수 변조되면 방송국 주파수는 상하로 변동합니다. 즉, fc에서 오디오 주파수와 같은 비율로 편차가 발생합니다. 이 주파수를 오디오 주파수 fa라고 합니다.
변조 중 방송국 RF 주파수가 변동하는 정도를 주파수 편차라고 하며, 델타(Δ) 기호를 사용합니다. 편차의 크기는 오디오 신호의 크기에 비례합니다. 변조 지수(mf)는 이전에 방송국 주파수가 (RF 주파수 스케일에서) 얼마나 편차가 있는지를 그 편차를 유발하는 오디오 신호의 주파수 fa로 나눈 비율로 정의되었습니다.
이 모든 것을 기호 형태로 간결하게 표현하면 다음과 같습니다.

변조 지수(mf)의 정의는 일정한 볼륨에서 낮은 오디오 주파수가 높은 mf 값을 발생시킨다는 것을 명확히 보여줍니다. 반대로 높은 오디오 주파수는 낮은 mf 값을 발생시킵니다. 하지만 이것이 중요할까요? 왜 이 변조 지수 값에 신경 써야 할까요? 잠시만 기다려 주십시오. 곧 mf 값이 효과적인 방송국 대역폭, 즉 각 방송국에 할당되는 채널 폭을 결정한다는 것을 알게 될 것입니다. 물론 채널이 넓을수록 스펙트럼의 메가헤르츠당 방송국 수가 줄어듭니다. 그리고 선형성 때문에 대역폭보다 훨씬 높은 반송파 주파수가 필요합니다.
음악이나 음성의 전송 대역폭을 고려하기 전에, 먼저 단일 톤 사인파 오디오 변조의 간단한 예를 살펴보겠습니다.
AM 요약
4장에서 AM을 살펴보았듯이, RF 반송파가 단일 오디오 주파수, 즉 사인파에 의해 진폭 변조될 때 두 개의 측파대 주파수가 생성됩니다. 이 측파대 주파수는 반송파 주파수 위아래로 동일한 간격으로 배치됩니다.
더 나아가 AM에서는 반송파 진폭은 변조에 의해 변하지 않지만, 측파대 진폭은 오디오 진폭에 비례합니다. 따라서 AM 송신기에서는 변조에 따라 총 출력 전력이 최대 50%까지 증가합니다.
FM 측파대
하지만 FM 시스템에서는 상황이 매우 다릅니다.
(a) FM 반송파의 진폭(즉, 중심 주파수 fc)은 전혀 일정하지 않습니다. 어떤 변조 조건에서는 반송파 전력이 0이 될 수도 있습니다.
(b) 총 출력 전력은 항상 일정합니다.
(c) 측파대의 진폭은 오디오의 진폭과 주파수 모두에 따라 달라집니다.
(d) 단일 톤(사인파) 오디오 변조 신호의 경우에도 주파수 변조는 (원칙적으로) 무한한 수의 측파대 주파수를 생성합니다. 이 주파수들은 그림 1에서 볼 수 있듯이 반송파 주파수 위아래로 쌍으로 분포하며, 오디오 주파수와 동일한 주파수 간격으로 배치됩니다.
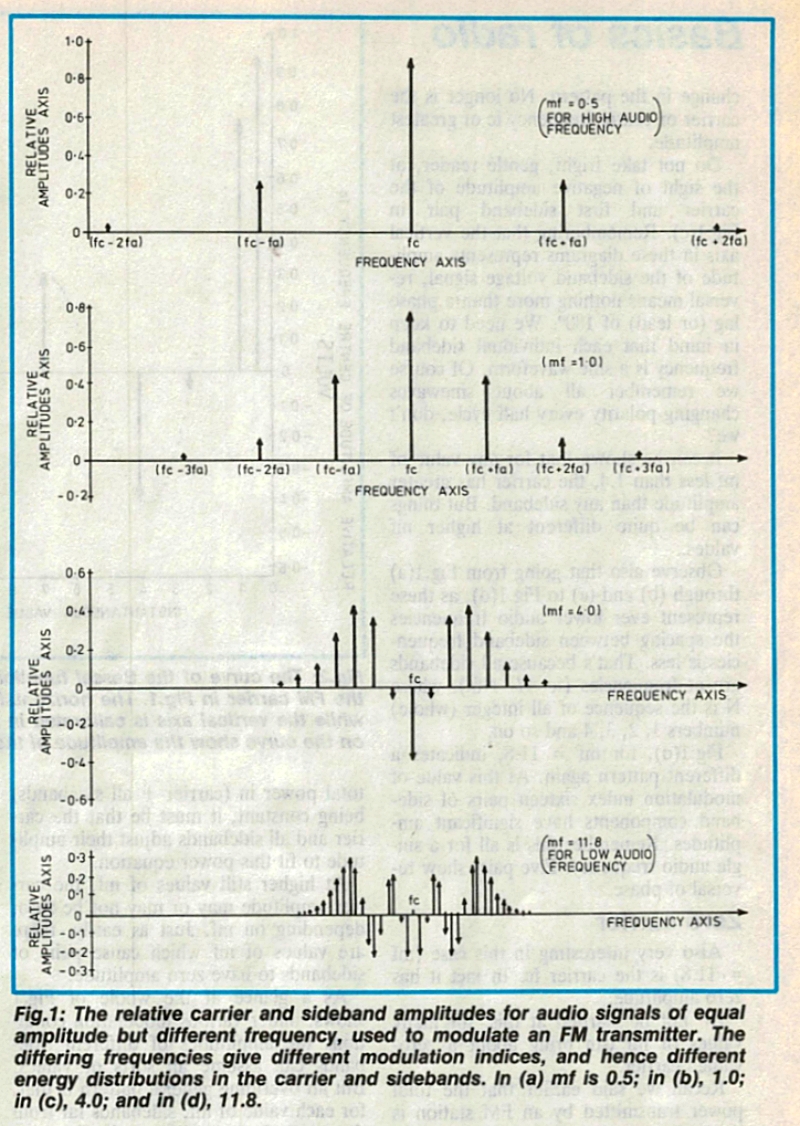
(e) 측파대 성분은 쌍의 집합으로 나타나며, 각 쌍은 반송파 위아래로 동일한 주파수 간격으로 배치됩니다.
(f) 어느 한 쌍에서 두 측파대의 진폭은 동일합니다.
(g) 하지만 서로 다른 쌍의 진폭은 매우 다양합니다.
(h) 각 측파대 쌍의 진폭은 변조 지수 mf의 다른 함수입니다.
(i) 반송파 fc의 진폭은 mf의 또 다른 함수입니다.
변조 지수 mf
그림 1(a, b, c, d)은 단일 톤 사인파 변조를 사용하여 네 가지 다른 mf 값에 의해 생성된 FM 측파대 주파수 패턴을 나타낸 것입니다. 세로축은 반송파와 측파대의 상대 진폭을 나타내고, 가로축은 무선 주파수를 나타냅니다. 모든 그래프는 동일한 축척으로 그려졌습니다.
많은 호주 FM 방송국은 최대 ±75kHz의 편차를 사용하며, 오디오 주파수 응답은 최대 15kHz입니다.
하지만 사용되는 변조 주파수는 이보다 높습니다. 방송국은 원래 오디오 신호 외에도 19kHz 파일럿 톤, 스테레오 ‘차이’ 신호, 그리고 종종 보조 정보 반송파를 전송합니다. 이러한 이유로 송신기에서는 변조 주파수가 최대 70kHz 또는 75kHz까지 확장될 수 있습니다. (스테레오, 파일럿 톤, 보조 송신은 이 시리즈의 후반부에서 논의합니다.)
주파수 편차(델타)가 75kHz이고 변조 주파수 fa = 75kHz일 때 주파수 변조 지수 mf는 다음과 같습니다.
mf = 델타/fa, 따라서
mf = 75kHz/75kHz
mf = 1.0
FM 방송국 외에도 다른 FM 송신기들이 있습니다. 원격 측정 시스템과 다중 채널 통신 링크는 훨씬 더 넓은 범위의 변조 주파수를 사용할 수 있습니다. 75kHz 편차를 사용하는 송신기가 150kHz 신호로 변조될 경우, mf는 다음과 같습니다.
mf = 75kHz/150kHz = 0.5 (최소)
그림 1(a)는 mf = 0.5이고 단일 톤 사인파 변조를 사용할 때 FM 송신에서 생성되는 측파대 패턴을 보여줍니다. 그림에서 세로축은 반송파 fc와 측파대의 상대 진폭을 나타냅니다.
여러 측파대
가로축은 반송파와 측파대의 주파수를 나타냅니다. 여러 측파대 주파수가 반송파 주파수 위아래로 동일한 간격으로 동일한 진폭 쌍으로 나타나는 것을 볼 수 있습니다. 이 간격은 오디오 주파수 fa와 같습니다. 따라서 측파대는 (fc+fa), (fc-fa), (fc+2fa), (fc-2fa) 등의 주파수에 나타납니다.
mf = 0.5일 때, 그림 1(a)는 원칙적으로 반송파 주파수 위아래(즉, 그림의 좌우)로 무한한 거리를 확장합니다. 따라서 표시된 것보다 훨씬 많은 측파대 주파수가 변조 주파수 fa의 모든 배수마다 간격을 두고 배치됩니다. 그러나 계산 결과 mf = 0.5일 때 첫 번째와 두 번째 쌍을 제외한 모든 측파대는 매우 낮은 진폭을 가집니다. 주파수(fc +/-3fa)에서 세 번째 측파대 쌍은 상대 진폭이 약 0.01에 불과한 반면, 네 번째 쌍(fc +/-4fa)은 약 0.003으로 매우 약합니다.
그런데 그림 1의 모든 다이어그램은 동일한 오디오 볼륨을 나타내기 위해 그려졌으며, 따라서 RF 편차 값도 동일합니다.
측파대 진폭
그림 1(a)는 매우 높은 오디오 주파수가 사용될 때의 상황을 나타냅니다. 그림 1(b, c, d)는 동일한 볼륨에서 오디오 주파수가 감소함에 따라 측파대의 변화 패턴을 점진적으로 보여줍니다.
그림 1(b)(그림 1(a)에 비해 오디오 주파수가 절반)는 mf = 1.0일 때 적어도 처음 세 쌍의 측파대에서 상당한 진폭을 보여줍니다.
그림 1(c)는 오디오 주파수가 그림 1(b)의 4분의 1로 감소했을 때의 효과를 보여줍니다. 이제 패턴에 큰 변화가 있음을 알 수 있습니다. 더 이상 반송파 또는 중심 주파수 fc가 가장 큰 진폭을 나타내지 않습니다.
친절한 독자 여러분, 그림 1(c)에서 반송파와 첫 번째 측파대 쌍의 음의 진폭을 보고 놀라지 마십시오. 이 다이어그램의 세로축은 측파대 전압 신호의 진폭을 나타내며, 반전은 180° 위상 지연(또는 진폭)을 의미합니다. 각 측파대 주파수는 사인파라는 점을 기억해야 합니다. 물론 사인파는 반주기마다 극성이 바뀐다는 것을 기억하고 있겠죠?
mf 값이 1.4 미만이면 반송파가 모든 측파대보다 진폭이 더 크다는 것을 보일 수 있습니다. 하지만 mf 값이 더 높으면 상황이 상당히 달라질 수 있습니다.
그림 1(a)에서 (b), (c)를 거쳐 그림 1(d)로 이동하면, 이 그림들은 점점 더 낮은 가청 주파수를 나타내므로 측파대 주파수 사이의 간격이 더 좁아집니다. 이는 모든 측파대가 (fc +/- Nfa) 주파수에 있기 때문입니다. 여기서 N은 1, 2, 3, 4 등의 모든 정수(정수)의 시퀀스입니다.
그림 1(d)의 mf = 11.8에 대해 ‘는 다시 다른 패턴을 나타냅니다. 이 변조 지수 값에서 16쌍의 측파대 성분이 상당한 진폭을 갖습니다. 이는 모두 단일 오디오 주파수에 대한 것임을 기억하십시오. 5쌍은 위상 반전을 나타냅니다.
제로 캐리어
이 경우(mf = 11.8)에서 매우 흥미로운 점은 캐리어 fc입니다. 실제로 진폭은 0입니다. 이에 놀라지 마십시오. mf 값이 많으면 캐리어 값이 0이 될 수 있습니다.
앞서 FM 방송국에서 송신하는 총 전력은 변조 주파수나 진폭에 관계없이 항상 일정하다고 언급했습니다. 이는 그림 l(a, b, c, d)에 나타난 송신기가 네 가지 경우 모두 동일한 전력을 출력한다는 것을 의미합니다. 그림 l(a와 b)에서 mf 값이 낮을 경우, 캐리어가 대부분의 전력을 전달하고 나머지 전력은 측파대에 있습니다.
mf = 4(그림 1(c))의 경우, 측파대는 방송국 전력의 상당 부분을 차지하며, 캐리어의 전력은 적습니다. 그러나 그림 1(d)처럼 mf = 11.8일 경우, 모든 전력은 측파대 집합에 의해 전달되고 캐리어에는 전력이 없습니다.
측파대의 어떤 조건에서든 (반송파 + 모든 측파대)의 총 전력이 일정하다면, 반송파와 모든 측파대는 이 전력 방정식에 맞게 진폭을 조정해야 합니다. mf 값이 더 높을수록, mf에 따라 반송파 진폭은 0일 수도 있고 아닐 수도 있습니다. 마찬가지로, 측파대 쌍의 진폭이 0이 되도록 하는 mf 값도 있습니다.
그림 1 전체를 살펴보면 알 수 있듯이, 다양한 변조 조건에서 서로 다른 측파대의 진폭은 다양한 값을 가질 수 있습니다. 그러나 가장 중요한 일반적인 패턴은 mf 값이 각일 때 반송파에서 멀리 떨어진 측파대의 진폭이 더 작다는 것입니다.
이러한 사실 때문에 모든 측파대를 전송할 필요가 없습니다. “그렇죠”라고 말할 수도 있습니다. “이러한 측파대를 무한히 방송하는 것은 불가능합니다!” FM 방송사는 반송파와 모든 주요 측파대를 전송합니다. FM 수신기에서 저왜곡으로 하이파이 음악을 재생할 수 있을 만큼 충분한 측파대를 수신합니다. 단일 톤 변조에는 이 모든 것이 좋습니다. 하지만 음악이나 음성은 여러 주파수 성분이 복잡하게 섞인 것이라는 사실은 누구나 알고 있으므로 이의를 제기할 수 있습니다.
맞습니다. 하지만 모든 복잡한 소리는 여러 사인파의 조합, 즉 단일 톤으로 표현될 수 있습니다. 이러한 주파수 성분은 다양한 진폭과 위상 차이를 갖습니다. 푸리에 분석과 그 외 여러 가지가 있습니다!
각 오디오 주파수 성분의 주파수와 음량, 그리고 변조 지수 mf의 합성값을 (힘들게) 계산할 수 있습니다. 여기서는 이 작업을 시도하지 않겠지만, 그 결과로 얼마나 다양한 측파대가 생성되는지 상상해 보세요. 그림 1(a, b, c, d)의 각 부분과 각 오디오 성분마다 하나씩, 수백 개의 다른 부분들을 중첩하면 수천 개의 측파대 주파수로 이루어진 미로 같은 그림을 그릴 수 있습니다.
방송국에 할당된 RF 채널에 포함되는 모든 부분이 전송됩니다. 일반적인 호주 수도 FM 방송국은 표 1에 표시된 것과 유사한 특성을 갖습니다.
VHF의 필요성
이제 FM 송수신에 있어 VHF 또는 UHF 작동의 중요성을 알게 되었습니다. 전송 대역폭은 매우 높아 최대 262kHz 또는 ±131kHz입니다. 앞서 시스템 선형성에 대해 언급했던 내용을 다시 생각해 보세요. 방송국의 송신기와 수신기 모두 반송파 주파수 fc에 동조된 공진 LC 회로를 찾을 수 있습니다. 동조된 회로는 반송파뿐만 아니라 (fc-131kHz)부터 (fc+131kHz)까지 모든 송신 측파대에도 응답해야 합니다.
동조된 회로는 중심 주파수 fc의 양쪽에 있는 아주 작은 부분만큼 떨어진 신호에 응답할 때만 적절한 Q를 유지할 수 있습니다. 원하는 측파대 범위를 충족하려면 ±131kHz가 FM 반송파 주파수 fc에 비해 매우 작아야 합니다. 일반적으로 1/500에서 1/1000 정도의 부분이 권장됩니다.
모든 호주 FM 방송국은 88MHz에서 108MHz 사이의 VHF 대역 어딘가에 반송 주파수를 할당받습니다. 일반적으로 ±131kHz의 전송 대역폭을 사용할 때, 대역폭 대 반송 주파수 비율은 (131kHz/88MHz) = 1/671에서 (131kHz/108MHz) = 1/824 사이로, 이는 만족스러운 수준입니다.
이것이 모든 호주 FM 방송국이 VHF 대역에서 제공되는 더 높은 주파수 대역에 위치하게 되는 진짜 이유입니다. 물론 미래에 FM 방송국이 (일부 해외처럼) UHF 대역의 더 높은 대역에 배치된다면, 그 비율은 더욱 향상될 것입니다.
설명
탐구심이 많은 독자라면 그림 1이 매우 예쁘다고 이의를 제기할 수도 있고, 물론 우리는 다중 측파대 개념을 받아들입니다. 그리고 각 측파대 간격이 가청 주파수 fa의 배수라는 점은 믿을 만합니다. 하지만 도대체 어디서 그 모든 이상한 반송파 및 측파대 진폭 값을 얻는 걸까요? 좋은 질문입니다!
사실 FM은 수학자들에게 정말 신나는 실험거리를 제공합니다. 여기서는 다루지 않겠지만(한숨!) 방정식은 전송 신호 전압이 사인파가 아니라는 것을 보여줍니다. 오히려 (사인의 사인) 함수 형태를 띠며, 이는 ‘제1종 베셀 함수’라고 불리는 무한한 곡선 집합을 생성합니다. 이 함수들은 J0, J1, J2 등의 기호로 표시되며, 각각은 변조 지수 mf에 대한 별도의 함수입니다.
이러한 함수 중 처음 네 개는 그림 1과 2에 나와 있습니다. 2, 3, 4, 5. 독자들이 모든 사진을 원하지 않을 거라는 걸 알고 있었습니다(맞춰보셨겠지만, 그 수는 무한합니다!). 첫 번째 곡선 Jo(mf)는 그림 2에 mf 값이 0에서 19까지일 때 나타납니다. 이 곡선은 다양한 mf 값에 대한 반송파 fc의 진폭을 보여주는 보정 곡선으로 사용됩니다. 그림 2에서 저자는 화살표가 있는 수직선을 그렸습니다. 전압 벡터도 좋습니다.
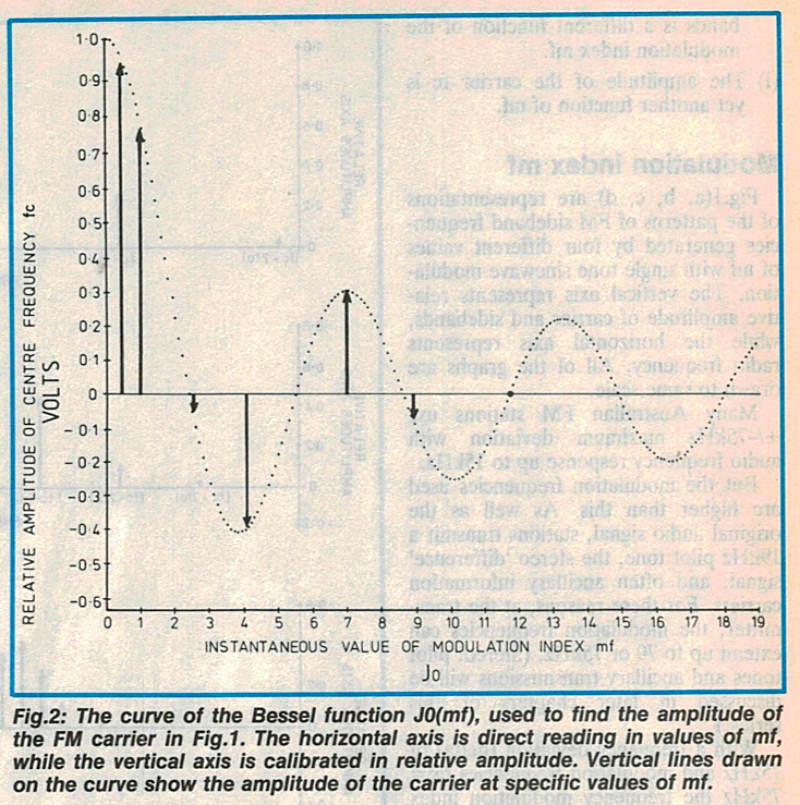
0.5에서 위쪽으로 그린 전압 벡터는 그림 2에서 mf 길이가 0.939인 지점입니다. 이는 그림 1(a)에서 mf = 0.5일 때 반송파의 상대 진폭을 나타냅니다.
마찬가지로, 그림 2에서 mf = 1.0, 4.0, 11.8인 지점에서 수직 전압 벡터를 그리면 그림 1(b)(mf 1.0), 그림 1(c)(mf 4.0), 그림 1(d)(mf = 11.8)을 그리는 데 사용할 수 있는 반송파 진폭 값을 얻을 수 있습니다. 덧붙여 그림 2는 mf 값이 1에서 19까지인 경우에만 베셀 함수를 사용하지만, 이 함수는 오른쪽으로 무한히 확장됩니다. 따라서 Jo(mf)를 사용하여 모든 mf 범위에서 반송파 진폭을 구할 수 있습니다.
그림 2를 보면 mf = 0.5일 때 그림 1(a)에서 반송파가 매우 크고, mf = 1.0일 때 그림 1(b)에서 반송파가 약간 작은 이유를 알 수 있습니다. 그림 1(c)에서 mf = 4.0일 때의 역상 반송파는 그림 2에서 mf = 4.0일 때 그려진 하향 전압 벡터로 설명할 수 있습니다.
그림 2의 Jo(mf)는 진동하는 연속 함수이고, 때로는 양수이고 때로는 음수이기 때문에 여러 지점에서 영점을 교차해야 합니다. 정수. 그림 2에서 mf = 11.8일 때 이러한 영점 교차가 하나 발생하며, 이것이 그림 1(d)에서 mf = 11.8일 때 반송파의 진폭이 0인 이유입니다.
마찬가지로, 다른 베셀 함수는 임의의 mf 값에 대해 측파대 쌍의 진폭을 나타내는 데 사용됩니다. 그림 3은 Jl(mf)라는 곡선을 보여주는데, 이는 첫 번째 측파대 주파수 쌍의 진폭을 나타냅니다. 그림 1(a, b, c, d)에서 첫 번째 측파대의 진폭을 구한 지점을 보여주기 위해 다시 여러 지점에 수직 전압 벡터를 그렸습니다.

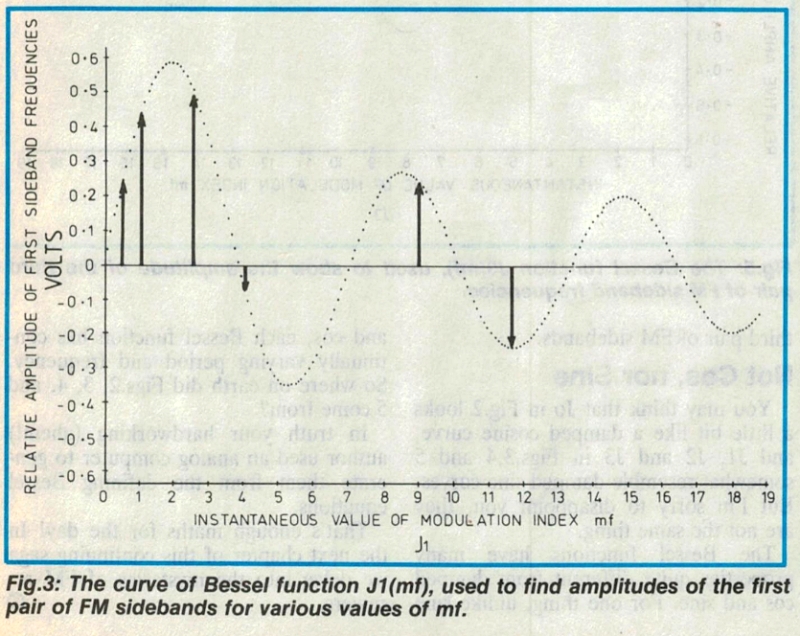
모든 베셀 함수는 진동하므로, 모든 측파대 쌍은 순방향 또는 역방향 위상을 가질 가능성이 높습니다. 즉, 그림 1과 같은 다이어그램에서 위쪽 또는 아래쪽으로 그려질 수 있습니다. 또한 모든 측파대 쌍은 서로 다른 mf 값에서 크거나, 작거나, 0의 진폭을 가질 수 있습니다.
같은 방법으로 그림 4의 곡선 J2(mf)는 모든 mf에 대한 두 번째 FM 측파대 쌍의 진폭 값을 나타냅니다. 그림 4에 그려진 수직선은 mf = 0.5, 1.0, 4, 11.8에 대한 전압 벡터를 나타냅니다. 이 벡터들은 그림 1(a, b, c, d)에서 두 번째 측파대 쌍의 높이를 나타내는 데 사용되었습니다.
그림 5는 곡선 J3(mf)를 보여주며, 세 번째 FM 측파대 쌍의 진폭도 비슷한 방식으로 나타냅니다.
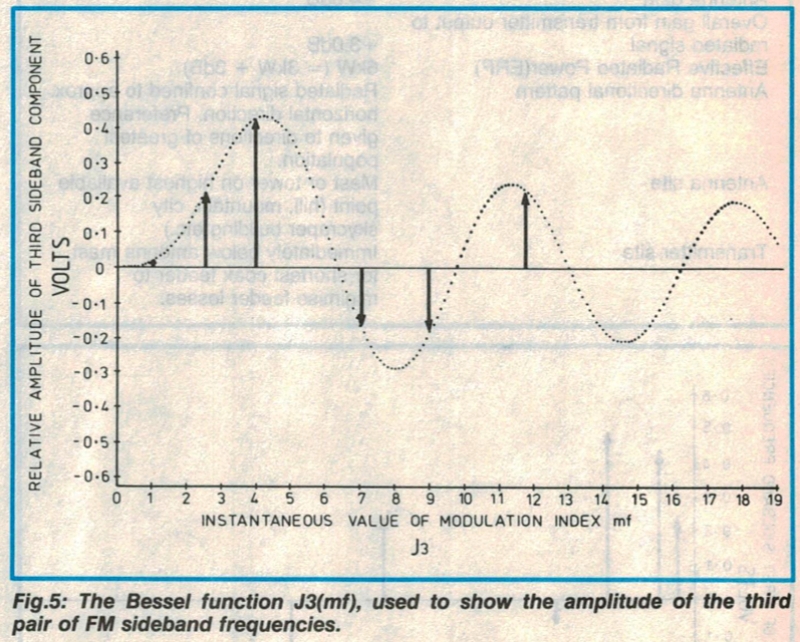
코사인도 아니고 사인도 아닙니다. 그림 2의 Jo는 감쇠 코사인 곡선처럼 보이고, 그림 3, 4, 5의 J1, J2, J3는 감쇠 사인 곡선과 다소 비슷하다고 생각하실 수도 있습니다. 하지만 실망스럽게도, 이 둘은 같은 것이 아닙니다.
베셀 함수는 감쇠 코사인 및 사인과는 상당히 다른 여러 속성을 가지고 있습니다. 우선, 사인 및 코사인과 달리 각 베셀 함수는 주기와 주파수가 지속적으로 변합니다. 그렇다면 그림 2, 3, 4, 5는 도대체 어디서 나온 것일까요?
사실, 당신의 노고(헛기침!) 저자는 정의하는 베셀 방정식을 사용하여 아날로그 컴퓨터를 사용하여 이들을 생성했습니다. 오늘의 수학 이야기는 여기까지입니다! 이 연재의 다음 장에서는 FM 수신기의 미스터리를 파헤쳐 보겠습니다.




