글쓴이 : SOONDORI
어떤 정리 문서에서… 양이 너무 많다. 눈에 걸리는 문단만 발췌 등록.
* 관련 글 : Analog Devices Basic Linear Design의 일부 (3), Modulator
섹션 8.3 : 시간 영역 응답
지금까지 논의는 주로 필터의 주파수 영역 응답에 초점을 맞춰 왔습니다. 특히 과도 조건에서 시간 영역 응답도 문제가 될 수 있습니다. 시간 영역과 주파수 영역 간 이동은 푸리에 변환과 라플라스 변환을 사용하여 수행됩니다. 이를 통해 비정현파 여기(excitation)에 대한 필터의 성능을 평가하는 방법이 제공됩니다. 필터의 전달 함수는 출력 시간 함수와 입력 시간 함수의 비율입니다. 필터의 임펄스 응답이 대역폭을 정의한다는 것을 알 수 있습니다. 시간 영역 응답은 많은 시스템, 특히 많은 변조 방식에서 진폭과 위상 정보를 모두 사용하는 통신 시스템에서 실질적인 고려 사항입니다.
● 임펄스 응답, Impulse Response
임펄스 함수는 면적이 1인 무한히 높고 무한히 좁은 펄스로 정의됩니다. 물론 이는 물리적인 관점에서 구현할 수 없습니다. 임펄스 폭이 필터의 상승 시간보다 훨씬 작으면 필터의 결과 응답은 필터 응답의 실제 임펄스 응답에 대한 합리적인 근사값을 제공합니다. 시간 영역에서 필터의 임펄스 응답은 주파수 영역에서 필터의 대역폭에 비례합니다. 임펄스가 좁을수록 필터의 대역폭은 넓어집니다. 펄스 진폭은 ωc/π와 같으며, 이는 필터 대역폭에도 비례합니다. 높이는 대역폭이 넓을수록 높아집니다. 펄스 폭은 2π/ωc와 같으며, 이는 대역폭에 반비례합니다. 진폭과 대역폭의 곱은 상수입니다.
라플라스 변환과 푸리에 변환을 사용하지 않고 필터의 응답을 계산하는 것은 쉽지 않습니다. 라플라스 변환은 곱셈과 나눗셈을 각각 덧셈과 뺄셈으로 변환합니다. 이 방법은 일반적으로 적분 및/또는 미분으로 구성된 방정식을 다루기 훨씬 쉬운 간단한 대수 방정식으로 변환합니다. 푸리에 변환은 반대 방향으로 작용합니다. 이 변환의 세부 사항은 여기서 논의하지 않습니다. 그러나 임펄스 응답과 필터 특성의 관계에 대한 몇 가지 일반적인 관찰을 할 것입니다. 언급한 바와 같이 임펄스 응답은 대역폭과 관련이 있음을 보일 수 있습니다. 따라서 진폭 판별력(원하는 신호를 다른 대역 외 신호 및 잡음과 구별하는 능력)과 시간 응답은 반비례합니다. 즉, 가장 좋은 진폭 응답을 갖는 필터는 가장 나쁜 시간 응답을 갖는 필터입니다. 모든 극점 필터의 경우, 체비셰프 필터가 가장 좋은 진폭 판별력을 제공하고, 그 다음으로 버터워스 필터, 베셀 필터 순입니다.
시간 영역 응답을 순위대로 나열하면 베셀 필터가 가장 좋고, 그 다음으로 버터워스 필터, 체비셰프 필터 순입니다. 다양한 필터 응답에 대한 자세한 내용은 다음 섹션에서 설명합니다. 임펄스 응답 또한 필터 차수가 증가함에 따라 증가합니다. 필터 차수가 높을수록 대역 제한이 커지고, 따라서 시간 응답이 저하됩니다. 다단 필터의 각 섹션은 고유한 임펄스 응답을 가지며, 전체 임펄스 응답은 개별 응답의 누적입니다. 시간 응답의 저하는 주파수 판별력이 증가함에 따라 개별 섹션의 Q가 증가하는 경향과도 관련이 있습니다. Q가 증가하면 개별 섹션의 오버슈트와 링잉이 증가하여 시간 응답이 길어집니다.

(▲ 존재하는 것 같지만 존재하지 않고, 존재하지 않는 것 같지만 있는 있는 것 같은? 개념과 공식으로 정의되는 임펄스를 현실에서 생성하려면… 사실은 불가능?)
* 관련 글 : Singer 91263-1, Impulse Generator
● 스텝 응답, Step Response
필터의 스텝 응답은 임펄스 응답의 적분입니다. 임펄스 응답에 적용되는 많은 일반론이 스텝 응답에도 적용됩니다. 계단 응답의 상승 시간의 기울기는 임펄스의 피크 응답과 같습니다. 필터 대역폭과 상승 시간의 곱은 상수입니다. 임펄스가 1과 같은 함수를 갖는 것처럼 계단 응답은 1/s와 같은 함수를 갖습니다. 이 두 표현식은 모두 무차원이므로 정규화할 수 있습니다. 필터의 계단 응답은 변조된 신호의 포락선 왜곡을 결정하는 데 유용합니다. 필터 계단 응답의 가장 중요한 두 가지 매개변수는 오버슈트와 링잉입니다. 좋은 펄스 응답을 위해서는 오버슈트가 최소화되어야 합니다. 링잉은 후속 펄스를 방해하지 않도록 가능한 한 빨리 감소해야 합니다. 실제 신호는 일반적으로 임펄스 펄스나 계단으로 구성되지 않으므로 과도 응답 곡선은 출력을 완전히 정확하게 추정하지 못합니다. 그러나 다양한 필터 유형의 과도 응답을 동등하게 비교할 수 있도록 하는 편리한 성능 지수입니다. 계단 응답과 임펄스 응답 계산은 수학적으로 복잡하기 때문에 컴퓨터로 가장 쉽게 수행할 수 있습니다. 많은 CAD(컴퓨터 지원 설계) 소프트웨어 패키지는 이러한 응답을 계산할 수 있는 기능을 갖추고 있습니다. 이러한 응답 중 일부는 다음 섹션에도 정리되어 있습니다. (이후 생략)
● 모든 극점 응답 비교
베셀, 버터워스, 체비셰프 등 여러 모든 극점(*) 필터의 응답(이 경우 0.5dB 리플)을 비교합니다. 8극 필터를 기준으로 비교합니다. 응답은 1Hz 차단 주파수에 대해 정규화되었습니다. 아래 그림 8.13과 8.14를 비교하면 응답 유형 간의 상충 관계를 쉽게 확인할 수 있습니다. 베셀 필터에서 버터워스 필터, 체비셰프 필터로 이동하면 과도 특성이 점차 악화됨에 따라 진폭 판별력이 향상되는 것을 확인할 수 있습니다. (이후 생략)
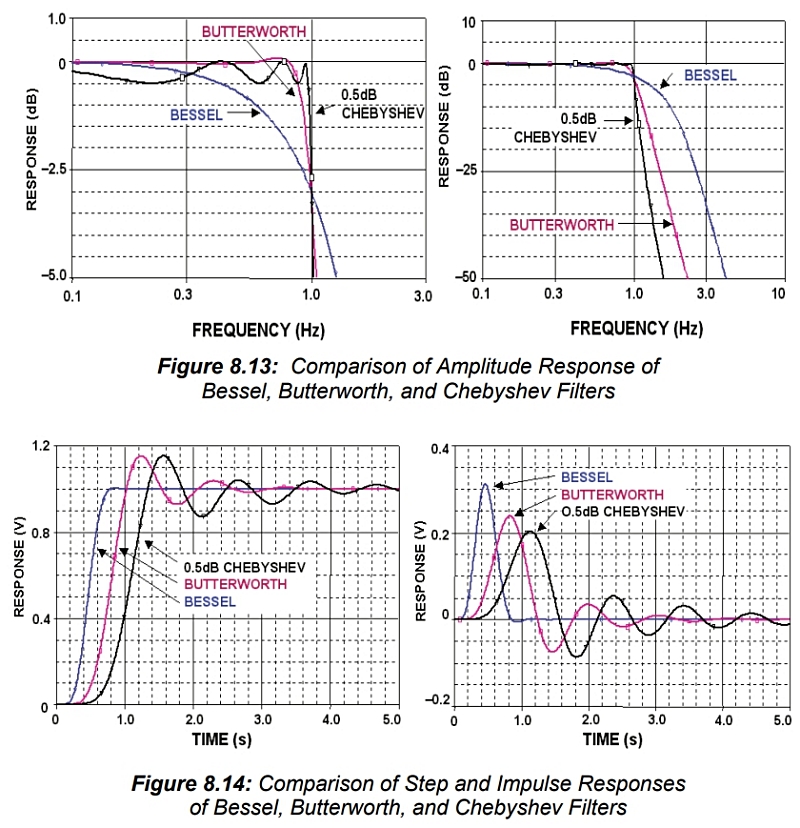
* Pole을 극점 또는 기둥, 뭐라고 해석하든… 트랜스퍼 펑션(=전달 함수)의 분모(극점) 또는 분자(영점)를 0으로 만드는 복소 주파수 ‘s’의 값. 이런 것은 말도 어렵고 계산하기도 어렵다. 그냥 시각적으로는… 마디마디 감쇄 포인트로 치부하기. 단극, 2극, 4극… 8극, 무한대 극으로 가면 갈 수록 무 자르듯. 낮을 수록 완만하게 칼질.
● 단극 RC 필터, Single Pole RC Filter
가장 간단한 필터 구성 요소는 수동 RC 섹션입니다. 단극은 저역 통과 또는 고역 통과일 수 있습니다. 기수 차수(*) 필터는 단극(註, 單極) 섹션을 갖습니다. 저역 통과 RC 섹션의 기본 형태는 그림 8.37(A)에 나와 있습니다.
* 次數, 영어로는 Order. 양파 껍질을 까고 있다고 상상하면, 첫 번째, 두 번째, 세 번째… 무한대.
부하 임피던스가 높다고 가정합니다(> ×10). 따라서 회로에 부하가 걸리지 않습니다. 부하는 필터의 션트 암과 병렬로 연결됩니다. 그렇지 않은 경우, 섹션은 연산 증폭기로 버퍼링해야 합니다. 저역 통과 필터는 저항과 커패시터를 교체하여 고역 통과 필터로 변환할 수 있습니다. 고역 통과 필터의 기본 형태는 그림 8.37(B)에 나와 있습니다. 이 경우에도 부하 임피던스가 높다고 가정합니다.
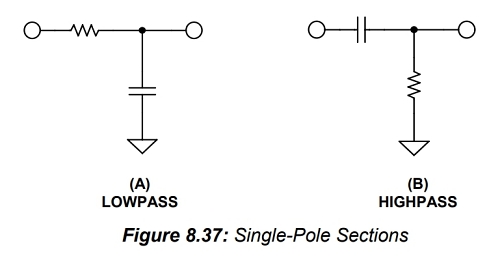
(▲ 튜너 디앰퍼시스 설정, 앰프 땡땡 필터, 스피커 음색 조작 등… 안 쓰이는 데가 없음. 그래서 WEB TOOL이 널려있다. 예를 들어, https://www.digikey.com/en/resources/conversion-calculators/conversion-calculator-low-pass-and-high-pass-filter)
단극은 증폭기 회로에도 통합될 수 있습니다. 그림 8.38(A)는 피드백 루프에 커패시터가 있는 증폭기 회로를 보여줍니다. 이는 저역 통과 필터를 형성하는데, 주파수가 증가함에 따라 유효 피드백 임피던스가 감소하여 이득이 감소하기 때문입니다.
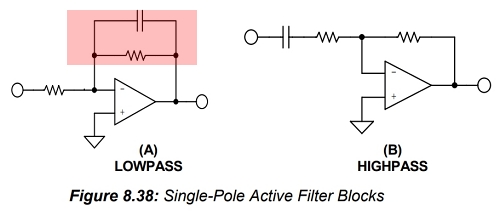
(▲ 흔히 FM 튜너의 Post Amp.에서, 디엠퍼시스를 지정하는 영역에서 볼 수 있음)
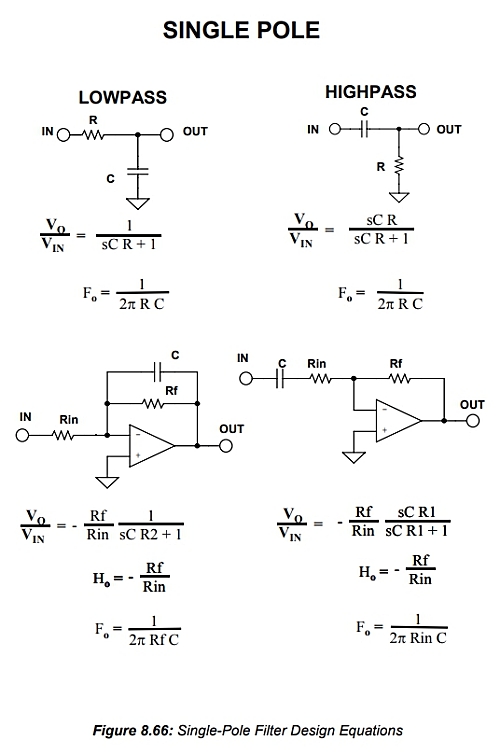
그림 8.38(B)는 입력 저항과 직렬로 연결된 커패시터를 보여줍니다. 이로 인해 신호는 직류(DC)에서 차단됩니다. 주파수가 직류에서 증가함에 따라 커패시터의 임피던스는 감소하고 회로의 이득은 증가합니다. 이는 고역 통과 필터입니다. 단극 필터의 설계 방정식은 그림 8.66에 나와 있습니다. (이후 생략)
● 적분기
피드백 네트워크에 주파수 의존 임피던스를 입력하면 역 주파수 응답이 발생합니다. 예를 들어, 주파수 의존 임피던스가 주파수 증가에 따라 감소하는 커패시터를 연산 증폭기의 피드백 네트워크에 입력하면
그림 8.44와 같이 적분기가 형성됩니다.
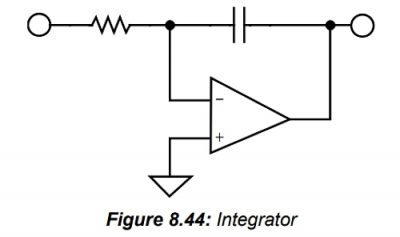
(▲ Accumulator 또는 작은 것을 쌓는 積分. 그렇게, 커패시터에 뭐가 계속 쌓인다. 그러면 그 다음 상황이 벌어진다는…)
적분기는 DC에서 높은 이득(즉, 연산 증폭기의 개방 루프 이득)을 갖습니다. 적분기는 차단 주파수가 0Hz인 저역 통과 필터로 생각할 수도 있습니다. (이후 생략)
● 섹션 8.7: 필터 구현의 실제 문제
이전 섹션에서는 필터를 수학적 함수로 다루었습니다. 필터 설계는 “완벽한” 구성 요소를 사용하여 구현되었다고 가정했습니다. 필터를 실제 구성 요소로 구축하는 경우 일반적으로 설계 상충 관계를 고려해야 합니다.
두 차수보다 큰 차수를 갖는 필터를 구축할 때는 여러 개의 2차 및/또는 1차 섹션이 사용됩니다. 이러한 섹션의 주파수와 Q는 정확하게 일치해야 하며, 그렇지 않으면 필터의 전체 응답에 영향을 미칩니다. 예를 들어, 다음 섹션의 안티앨리어싱 필터 설계 예시는 5차 버터워스 필터로, 주파수(Fo) = 1이고 Q = 1.618인 2차 섹션, 주파수(Fo) = 1이고 Q = 0.618인 2차 섹션, 그리고 주파수(Fo) = 1인 1차 섹션으로 구성됩니다(필터는 1 rad/sec로 정규화됨). 어떤 섹션의 Q 또는 주파수 응답이 약간 어긋나면 전체 응답이 원하는 응답에서 벗어날 수 있습니다. 근사할 수는 있지만 정확하지는 않습니다. 엔지니어링에서 일반적으로 그렇듯이, 어떤 절충안을 선택해야 할지 결정해야 합니다.
예를 들어, 특정 응답이 정말 필요한가요? 통과 대역에 리플이 조금 더 많으면 문제가 될까요? 또는 차단 주파수가 약간 다른 주파수에 있는 경우 문제가 될까요? 이러한 유형의 질문은 설계자가 직면하는 질문이며, 설계마다 다릅니다. (이후 생략)
● 수동 부품(저항, 커패시터, 인덕터)
수동 부품은 가장 먼저 해결해야 할 문제입니다. 필터를 설계할 때 부품의 계산된 값은 상용 제품에서 구할 수 없을 가능성이 높습니다. 저항, 커패시터, 인덕터는 표준 값으로 제공됩니다. 맞춤 값을 주문할 수 있지만, 실제 허용 오차는 기껏해야 ± 1% 정도일 것입니다. 다른 방법은 표준 값의 직렬 및/또는 병렬 조합을 사용하여 필요한 값을 만드는 것입니다. 이로 인해 필터의 비용과 크기가 증가합니다. 부품 비용이 증가할 뿐만 아니라 필터 로딩 및 튜닝에 드는 제조 비용도 증가합니다. 또한, 성공 여부는 사용되는 부품 수, 허용 오차, 그리고 온도 및 시간에 따른 추적 성능에 따라 제한될 것입니다. 더 실용적인 방법은 회로 분석 프로그램을 사용하여 표준 값을 사용하여 응답을 결정하는 것입니다. 이 프로그램은 온도에 따른 부품 드리프트의 영향을 평가할 수도 있습니다. 민감한 부품의 값은 필요한 경우 병렬 조합을 사용하여 조정하여 응답이 원하는 한계 내에 도달할 때까지 조정합니다. 많은 고급 필터 CAD 프로그램에 이 기능이 포함되어 있습니다. 필터의 공진 주파수와 Q는 일반적으로 부품 값에 의해 결정됩니다. 부품 값이 드리프트되면 필터의 주파수와 Q도 드리프트되고, 이로 인해 주파수 응답이 변하게 됩니다. 이는 특히 고차 필터에서 그렇습니다.
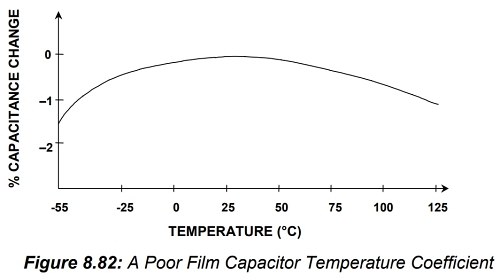
차수가 높을수록 Q 섹션이 높아집니다. Q 섹션이 높을수록 부품 값이 더 중요해집니다. Q는 일반적으로 두 개 이상의 부품, 일반적으로 커패시터의 비율로 설정되기 때문입니다. 부품의 초기 허용 오차 외에도 온도/시간 드리프트의 영향도 평가해야 합니다. 다양한 부품의 온도 계수는 크기와 부호가 다를 수 있습니다. 특히 커패시터는 드리프트가 있을 뿐만 아니라 온도 계수(TC)도 온도의 함수이기 때문에 어렵습니다. 그림 8.82와 같습니다. 이는 (비교적) 성능이 좋지 않은 필름 커패시터의 온도 계수를 나타내며, 폴리에스터 또는 폴리카보네이트 유형에서 일반적으로 나타날 수 있습니다. 필름 커패시터의 선형 TC는 폴리스티렌, 폴리프로필렌 및 테플론 유전체에서 찾을 수 있습니다. 이러한 유형의 TC는 100ppm/°C에서 200ppm/°C 정도이며, 필요한 경우 회로의 다른 곳에 보완적인 TC를 사용하여 보상할 수 있습니다.
100Ω 미만의 저항 값은 피해야 하며, 1MΩ 이상의 저항 값도 마찬가지입니다. 매우 낮은 저항 값(100Ω 미만)은 많은 구동 전류를 필요로 하고 많은 전력을 소모할 수 있습니다. 이 두 가지 모두 피해야 합니다. 또한 낮은 저항 값과 매우 큰 저항 값은 쉽게 구할 수 없을 수 있습니다. 매우 큰 저항 값은 기생 성분에 더 취약한 경향이 있는데, 작은 커패시턴스가 더 큰 임피던스 레벨로 더 쉽게 결합되기 때문입니다.
잡음은 저항 값의 제곱근에 따라 증가합니다. 또한 큰 저항 값은 증폭기 바이어스 전류의 영향으로 더 큰 오프셋을 발생시킵니다. 회로 레이아웃 및 기타 요인으로 인한 기생 커패시턴스는 회로 성능에 영향을 미칩니다. 기생 커패시턴스는 PC 보드의 두 트레이스 사이(보드의 같은 면 또는 반대쪽), 인접한 부품의 리드 사이, 그리고 생각할 수 있는 (그리고 대부분의 경우 생각할 수 없는) 거의 모든 곳에서 형성될 수 있습니다. 이러한 정전용량은 일반적으로 작기 때문에 고임피던스 노드에서 그 영향이 더 큽니다. 따라서 회로의 임피던스를 낮게 유지함으로써 대부분의 경우 제어할 수 있습니다. 부유 정전용량의 영향은 주파수에 따라 달라지며, 고주파수에서 더욱 심해집니다. 주파수가 증가함에 따라 임피던스가 감소하기 때문입니다. 기생 성분은 외부 요인과 관련이 있을 뿐만 아니라 부품 자체에도 존재합니다. (이후 생략)
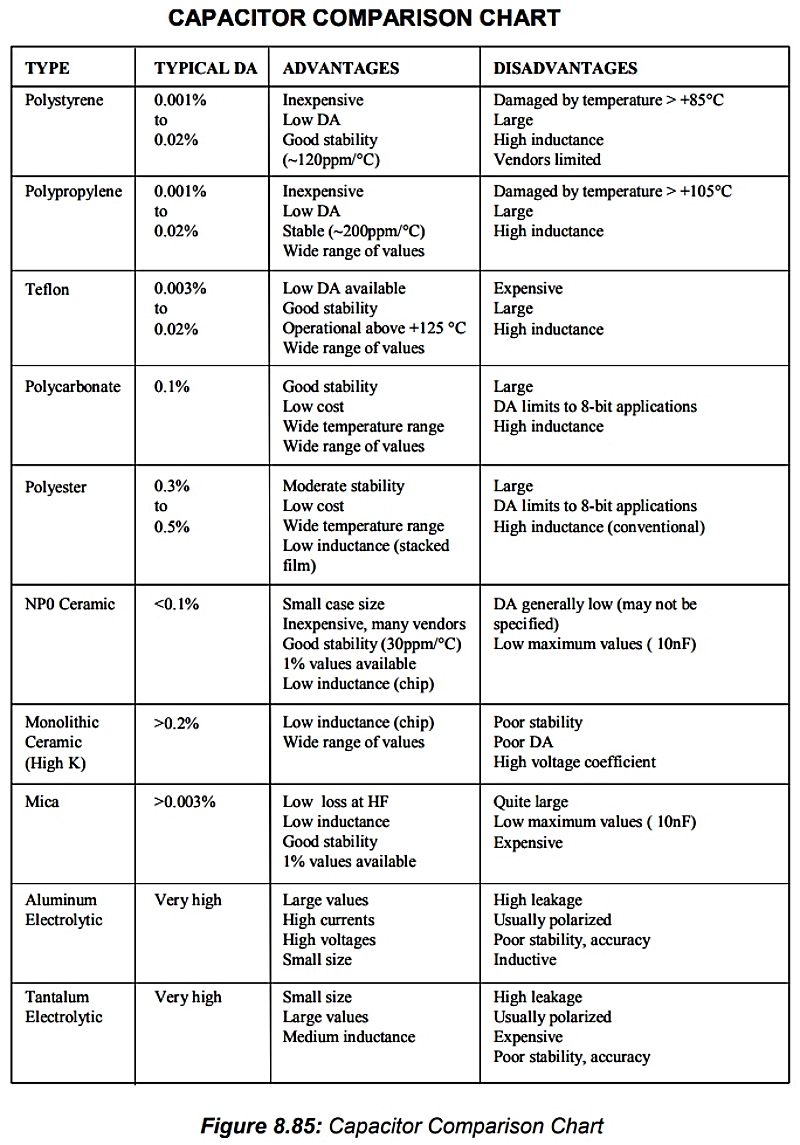
* 관련 글 : Analog Devices Basic Linear Design의 일부 (5), 커패시터




